In the world of data science and machine learning, the ability to organize and make sense of vast amounts of data is crucial. This is where clustering algorithms come into play. These sophisticated techniques allow us to group data into meaningful segments, uncover hidden patterns, and gain valuable insights. Clustering algorithms such as K-means clustering, hierarchical clustering, and DBSCAN are fundamental tools in data mining, segmentation, and big data analytics. Whether you’re diving into unsupervised learning for the first time or looking to refine your current data analysis strategies, understanding these clustering methods is essential for anyone working in this field. Let’s explore the intricate dynamics of clustering algorithms and their applications in various industries.

Introduction to Clustering in Data Science

Clustering is a pivotal technique in data science aimed at partitioning a dataset into distinct groups or clusters, where data points within the same group exhibit higher similarity to each other compared to those in different groups. This process is a form of unsupervised learning because it does not require pre-labeled data for training. Instead, it discovers hidden patterns or intrinsic structures within the data itself.

One of the most attractive aspects of clustering is its versatility across various domains and applications. From segmenting customers based on purchasing behavior in marketing to identifying distinct groups of genes with similar expression patterns in bioinformatics, clustering algorithms unlock insights that drive decision-making and strategy.

Consider large datasets in big data analytics—clustering can simplify the data complexity by reducing millions of data points to a few meaningful clusters. This not only aids in better data visualization but also enables more efficient data processing and analysis.

Different clustering methods address varying needs and datasets, each with its own strengths, weaknesses, and specific use cases. For example, K-means clustering is renowned for its speed and efficiency on large datasets, making it a popular choice in numerous practical applications. Hierarchical clustering, on the other hand, builds nested clusters and offers a more informative visual representation of data through dendrograms, though it may become computationally intensive with larger datasets.

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) presents another powerful alternative, particularly well-suited for data with noise or varying density. Unlike K-means, DBSCAN doesn’t require specifying the number of clusters beforehand and is adept at finding clusters of arbitrary shape.

Tools and libraries across various programming environments facilitate the implementation of these clustering algorithms in data science projects. For instance, libraries like Scikit-learn in Python provide a comprehensive suite for clustering, including K-means, hierarchical clustering, and DBSCAN. The abundance of such tools empowers data scientists to select the most appropriate algorithm tailored to their specific data and research needs.

In summary, clustering is an integral unsupervised learning approach in data science that extracts valuable patterns from raw data, enabling nuanced analysis and application across a multitude of fields. Through various clustering techniques and accessible tools, data scientists can effectively group data and derive meaningful insights that support informed decision-making.

Understanding Different Clustering Techniques

Clustering algorithms are a quintessential tool in the arsenal of data scientists, enabling the segmentation of datasets into meaningful groups based on underlying patterns. Various clustering techniques offer different ways to approach this segmentation, each with its strengths, weaknesses, and ideal use cases. Here’s a closer look at some key clustering methods in the field of machine learning:

1. Partitioning Methods: The most well-known example here is K-means clustering, which divides the data into (k) clusters by minimizing the variance within each cluster. This technique is highly suited for large datasets where the number of clusters (k) is known. However, it assumes spherical clusters of similar size and density, which may not always be the case.

   from sklearn.cluster import KMeans
   import numpy as np
   
   # Create a sample dataset
   data = np.array([[1.0, 2.0], [1.5, 1.8], [5.0, 8.0], [8.0, 8.0]])
   
   # Initialize KMeans with 2 clusters
   kmeans = KMeans(n_clusters=2)
   kmeans.fit(data)
   
   print("Cluster Centers:", kmeans.cluster_centers_)
   print("Labels:", kmeans.labels_)
   

   In this snippet, KMeans from scikit-learn is used to cluster a small dataset into two groups, showing the cluster centers and labels for each data point.

2. Hierarchical Clustering: This approach builds nested clusters by either merging or splitting them successively. It is subdivided into Agglomerative and Divisive clustering. Agglomerative clustering, the more common approach, begins with each data point as a single cluster and merges them until there is one cluster left or the predefined number of clusters is achieved. This method forms a tree-like structure called a dendrogram, making it easier to understand data relationships at various levels of granularity.

   from scipy.cluster.hierarchy import dendrogram, linkage
   import matplotlib.pyplot as plt
   
   # Generate hierarchical clustering data
   Z = linkage(data, 'ward')
   
   # Plot Dendrogram
   plt.figure()
   dendrogram(Z)
   plt.show()
   

3. Density-Based Techniques: DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a popular example. It clusters points that are closely packed together while marking points in low-density regions as outliers. This method is highly effective for datasets with varying cluster shapes and is less sensitive to noise compared to K-means.

   from sklearn.cluster import DBSCAN
   
   # Initialize DBSCAN
   dbscan = DBSCAN(eps=2, min_samples=2)
   dbscan.fit(data)
   
   print("Core Sample Indices:", dbscan.core_sample_indices_)
   print("Labels:", dbscan.labels_)
   

4. Grid-Based Clustering: Methods like STING (Statistical Information Grid) partition the data space into a grid structure, performing clustering operations on these partitions. This approach is beneficial for large datasets because of its computational efficiency.
5. Model-Based Clustering: Methods such as Gaussian Mixture Models (GMM) assume that data is generated by a mixture of several Gaussian distributions. This algorithm not only provides probabilistic cluster assignments but can model clusters of different shapes and sizes better than K-means.

   from sklearn.mixture import GaussianMixture
   
   # Initialize Gaussian Mixture Model with 2 components
   gmm = GaussianMixture(n_components=2)
   gmm.fit(data)
   
   print("Means:", gmm.means_)
   print("Predict labels:", gmm.predict(data))
   

Each clustering technique has its own unique advantages and is more suitable for particular types of data and specific use cases. Choosing the right clustering method largely depends on the dataset’s characteristics and the specific requirements of the analysis. For further details, you can explore the scikit-learn clustering documentation to understand the full breadth of clustering algorithms implemented in Python.

Exploring K-Means Clustering and Its Applications

K-Means clustering is one of the most widely used unsupervised learning methods for partitioning a dataset into K distinct, non-overlapping subsets or clusters. This algorithm aims to minimize the variance within each cluster, leading to tighter, more homogeneous groupings of data. The key idea behind K-Means is to identify K centroids, one for each cluster, and then maximize the distance between them.

The K-Means Clustering Algorithm: How It Works

1. Initialization: Select K initial centroids randomly from the dataset.
2. Cluster Assignment: Assign each data point to its nearest centroid based on the Euclidean distance.
3. Centroid Update: Recalculate the centroids as the mean of all points assigned to that particular cluster.
4. Iteration: Repeat steps 2 and 3 until the centroids no longer change significantly or a predefined number of iterations is reached.

Example Implementation in Python

Here is a simple Python implementation using sci-kit-learn’s KMeans:

from sklearn.cluster import KMeans
import numpy as np

# Sample data
X = np.array([[1, 2], [1, 4], [1, 0], 
              [4, 2], [4, 4], [4, 0]])

# Apply K-Means
kmeans = KMeans(n_clusters=2, random_state=0).fit(X)

print("Cluster centers:", kmeans.cluster_centers_)
print("Labels:", kmeans.labels_)

Applications of K-Means Clustering

Customer Segmentation

K-Means is extensively used in marketing to segment customers into distinct groups based on purchasing behavior, demographics, or browsing data. By identifying and understanding these segments, businesses can tailor their marketing strategies and improve customer experiences.

Image Compression

In computer vision, K-Means clustering is applied to image compression. Each pixel in an image can be treated as a data point, and the algorithm clusters these points, reducing the unique values to a limited number of centroids. This process decreases the image file size while preserving its visual quality.

from sklearn.datasets import load_sample_image
import matplotlib.pyplot as plt

# Load sample image and preprocess
china = load_sample_image("china.jpg")
data = china / 255.0  # Normalize pixel values
data = data.reshape(-1, 3)

# Apply K-Means clustering
kmeans = KMeans(n_clusters=64, random_state=0).fit(data)

# Replace each pixel with its cluster centroid
compressed_image = kmeans.cluster_centers_[kmeans.labels_]
compressed_image = compressed_image.reshape(china.shape)

# Display original and compressed images
plt.figure(figsize=(6, 3))

plt.subplot(121)
plt.title("Original Image")
plt.imshow(china)

plt.subplot(122)
plt.title("Compressed Image")
plt.imshow(compressed_image)

plt.show()

Anomaly Detection

K-Means clustering can also be leveraged for anomaly detection by identifying data points that do not fit well into any cluster. These outliers can then be flagged for further investigation.

from sklearn.preprocessing import StandardScaler

# Sample dataset with anomalies
X = np.array([[1, 2], [1, 4], [1, 0], 
              [4, 2], [4, 4], [4, 0], [10, 10]])

# Standardize data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Apply K-Means
kmeans = KMeans(n_clusters=2, random_state=0).fit(X_scaled)

# Compute distances from each point to its cluster center
distances = kmeans.transform(X_scaled)
# Distance from the assigned cluster's center
distances = distances[np.arange(len(X_scaled)), kmeans.labels_]

# Threshold for anomaly detection
threshold = distances.mean() + 2 * distances.std()

anomalies = X[distances > threshold]
print("Anomalies detected:\n", anomalies)

Choosing the Right Number of Clusters

A common challenge in K-Means clustering is determining the optimal number of clusters. Various methods like the Elbow Method and Silhouette Scores are commonly used. The Elbow Method involves plotting the explained variance as a function of the number of clusters and picking the ‘elbow’ point where the variance reduction sharply diminishes. Silhouette Scores measure how similar an object is to its own cluster compared to other clusters, with higher average silhouette scores indicating better-defined clusters.

from sklearn.metrics import silhouette_score

# Fit multiple K-Means models with different values of K
range_n_clusters = [2, 3, 4, 5, 6]
best_k = 0
best_score = -1
for n_clusters in range_n_clusters:
    kmeans = KMeans(n_clusters=n_clusters, random_state=0)
    kmeans.fit(X)
    score = silhouette_score(X, kmeans.labels_)
    print(f"For n_clusters = {n_clusters}, silhouette score is {score}")
    if score > best_score:
        best_score = score
        best_k = n_clusters

print(f"The best number of clusters is {best_k} with a silhouette score of {best_score}")

With its simplicity and practical applications across various fields, K-Means clustering serves as a foundational tool for data scientists and machine learning practitioners alike. However, it’s essential to recognize its limitations, such as sensitivity to initial centroids and the assumption that clusters are spherical and equally sized.

For further references and detailed examples, explore the scikit-learn documentation on K-Means Clustering.

The Mechanics of Hierarchical Clustering

Hierarchical clustering is a powerful and intuitive method for partitioning datasets into meaningful groups by building a hierarchy of clusters. Unlike other clustering algorithms, hierarchical clustering does not require the user to predefine the number of clusters. Instead, it generates a nested sequence of partitions in the form of a tree or dendrogram.

Algorithm Types

Hierarchical clustering comes in two primary forms: agglomerative (bottom-up) and divisive (top-down).

1. Agglomerative Hierarchical Clustering (AHC):
   • Step 1: Start with each observation as its own singleton cluster.
   • Step 2: Iterate by merging the closest pair of clusters until only one cluster remains or a stopping criterion is met.
   • Uses a variety of linkage criteria to determine which clusters to merge, such as single linkage (minimum distance), complete linkage (maximum distance), average linkage (average distance), and Ward’s method (minimizing variance).
2. Divisive Hierarchical Clustering:
   • Step 1: Begin with all observations in a single cluster.
   • Step 2: Recursively split clusters until each observation is its own singleton cluster or another stopping criterion is satisfied.

Distance Metrics

Distance metrics play a critical role in hierarchical clustering. Common choices include Euclidean distance, Manhattan distance, and cosine similarity. The choice of metric can significantly influence the resulting clusters.

Linkage Criteria

Linkage criteria determine how the distance between clusters is computed:

• Single Linkage: Measures the minimum distance between points in the two clusters.
• Complete Linkage: Measures the maximum distance between points in the two clusters.
• Average Linkage: Measures the average distance between points in the two clusters.
• Ward’s Method: Utilizes variance minimization to form clusters.

Dendrogram Construction

A dendrogram visually represents the hierarchical relationships between clusters. Nodes represent clusters, and their heights indicate the distance at which clusters were merged. Dendrograms help identify the optimum number of clusters by examining where large vertical distances occur.

from scipy.cluster.hierarchy import dendrogram, linkage
import matplotlib.pyplot as plt

# Sample data
data = [[1, 2], [2, 3], [3, 4], [5, 8], [8, 8], [9, 10]]

# Generate linkage matrix
linked = linkage(data, method='ward')

# Plot dendrogram
plt.figure(figsize=(10, 7))
dendrogram(linked, labels=['A', 'B', 'C', 'D', 'E', 'F'])
plt.show()

Computational Complexity

Hierarchical clustering, especially with agglomerative techniques, can be computationally intensive, with a time complexity of (O(n^3)) and space complexity of (O(n^2)) for large datasets. However, optimizations and approximations, such as the nearest point algorithm, can mitigate these challenges.

Practical Applications

Hierarchical clustering is widely used in various fields, including:

• Bioinformatics: For phylogenetic tree construction and gene expression data analysis.
• Market Segmentation: To identify customer segments based on purchasing behaviors.
• Document Clustering: To organize large collections of documents based on content similarity.

Links and further reading:

• SciPy Hierarchical Clustering
• Scikit-learn Hierarchical Clustering

Hierarchical clustering offers a robust way to find natural groupings in data, providing insights that are easily interpretable and useful across many domains.

DBSCAN: A Density-Based Clustering Approach

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a powerful density-based clustering method widely used in data mining and machine learning. Unlike K-Means clustering, which relies on defining the number of clusters a priori, DBSCAN can define clusters based on the density of data points, making it particularly effective at discovering arbitrarily shaped clusters and handling noise within data sets.

The Core Concept of DBSCAN

At its core, DBSCAN operates by identifying dense regions of data points, grouping them into clusters where the density exceeds a predefined threshold. This threshold is typically defined by two parameters: epsilon (ε)—specifying the radius of the neighborhood around a data point—and minPoints—the minimum number of data points required to form a dense region (cluster).

1. Core Points: Points that have at least minPoints data points within their ε-radius.
2. Border Points: Points that are within the ε-radius of a core point but themselves have fewer than minPoints points within their ε-radius.
3. Noise Points: Points that are neither core points nor border points and do not belong to any cluster.

DBSCAN Algorithm Steps:

1. Select a point: If it hasn’t been visited, calculate the ε-neighborhood.
2. Density Check: If the selected point has minPoints within its ε-neighborhood, it becomes a core point, and a new cluster is initiated.
3. Expand Cluster: Add all density-reachable points to this cluster. This involves recursively inspecting the ε-neighborhoods of each core point.
4. Mark Noise: Points that don’t qualify as part of any cluster are marked as noise.
5. Repeat: Continue until all points in the dataset have been visited.

Here’s a basic implementation of DBSCAN in Python, utilizing the scikit-learn library:

from sklearn.cluster import DBSCAN
import numpy as np

# Sample data
X = np.array([
    [1, 2],
    [2, 2],
    [2, 3],
    [8, 7],
    [8, 8],
    [25, 80]
])

# Apply DBSCAN
db = DBSCAN(eps=3, min_samples=2).fit(X)

# Labels of clusters, where -1 indicates noise
labels = db.labels_

print(labels)

Key Advantages and Limitations

Advantages:

• No Predefined Number of Clusters: No need to specify the number of clusters upfront.
• Arbitrary Shape Detection: Effective for clusters with non-linear shapes.
• Noise Handling: Ability to detect and handle noise, making it robust against outlier data points.

Limitations:

• Parameter Sensitivity: The algorithm’s effectiveness heavily depends on the choice of ε and minPoints, which might not be intuitive and can require domain-specific knowledge or heuristic methods for determination.
• Performance: With large datasets and high-dimensional data, the computational complexity can be a concern, though optimizations and parallel implementations can mitigate this issue.

Practical Applications of DBSCAN

DBSCAN is extensively used in various domains:

• Geospatial Data Analysis: Identifying regions with high-density locations, such as hotspots in crime data.
• Image Processing: Segmenting images based on pixel intensity.
• Market Segmentation: Determining distinct buyer segments in marketing data without predefined boundaries.
• Anomaly Detection: Identifying outliers or unusual patterns in datasets.

Alternatives and Extensions

While DBSCAN is effective for certain scenarios, alternatives might be considered under different contexts. For instance:

• OPTICS (Ordering Points To Identify the Clustering Structure): Overcomes the limitation of fixed ε by varying it to find an optimal structure.
• HDBSCAN (Hierarchical DBSCAN): Extends DBSCAN with a hierarchical approach, allowing a more detailed exploration of the cluster structure.

The detailed understanding of DBSCAN, alongside practical implementations and alternatives, ensures comprehensive cluster analysis tailored to specific needs and datasets. For further details, refer to the official scikit-learn documentation on DBSCAN.

Evaluating Clustering Methods and Their Effectiveness

Evaluating the effectiveness of clustering methods is a crucial step in any cluster analysis workflow. Without proper evaluation, it’s challenging to ascertain the quality and utility of the clusters produced. Here are some key techniques and metrics commonly employed to evaluate clustering methods:

Intrinsic Evaluation Metrics

1. Silhouette Score

The Silhouette Score measures how similar an object is to its own cluster compared to other clusters. It ranges from -1 to 1, with higher values indicating better-defined clusters. The formula for calculating the Silhouette Score for a sample is:

where:

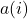• is the average distance between the sample 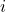and all other points in the same cluster.
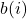• is the minimum average distance between the sample 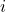and all other points in different clusters.

from sklearn.metrics import silhouette_score
# Assuming `X` is the dataset and `labels` are the clustering labels
score = silhouette_score(X, labels)
print(f'Silhouette Score: {score}')

2. Dunn Index

The Dunn Index aims to identify clusters that are compact and well-separated. It is computed as the ratio of the minimum inter-cluster distance to the maximum intra-cluster distance:

where:

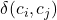• is the distance between centroids of clusters 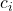and .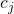
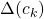• is the diameter of cluster .

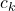Extrinsic Evaluation Metrics

1. Adjusted Rand Index (ARI)

ARI measures the similarity between the clusters produced by the algorithm and a ground truth class assignment, adjusting for chance groupings.

where RI is the Rand Index, and is its expected value.

from sklearn.metrics import adjusted_rand_score
# Assuming `true_labels` are the ground truth and `labels` are the predicted clustering labels
ari = adjusted_rand_score(true_labels, labels)
print(f'Adjusted Rand Index: {ari}')

2. Normalized Mutual Information (NMI)

NMI quantifies the amount of shared information between the cluster assignments and the ground truth, normalized to be between 0 and 1.

where is the mutual information between true labels U and predicted labels V, and and are the entropies of U and V.

from sklearn.metrics import normalized_mutual_info_score
# Assuming `true_labels` are the ground truth and `labels` are the predicted clustering labels
nmi = normalized_mutual_info_score(true_labels, labels)
print(f'Normalized Mutual Information: {nmi}')

Visual Evaluation Techniques

1. Elbow Method

The Elbow Method is used with algorithms like K-means clustering to determine the optimal number of clusters. This involves plotting the sum of squared distances from each point to its assigned cluster center and looking for an “elbow” point where the rate of decrease sharply slows.

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k).fit(X)
    sse.append(kmeans.inertia_)

plt.plot(range(1, 11), sse)
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()

2. Cluster Visualization

Visualizations like t-SNE or PCA can help in examining the cluster distribution visually, providing intuition about the clustering quality.

from sklearn.decomposition import PCA
import seaborn as sns

pca = PCA(n_components=2)
reduced_data = pca.fit_transform(X)
sns.scatterplot(x=reduced_data[:,0], y=reduced_data[:,1], hue=labels, palette='viridis')
plt.show()

Considerations for Effective Evaluation

The choice of clustering metrics should be aligned with the specific objectives and characteristics of the dataset. For instance, Silhouette Score and Dunn Index are internal measures not requiring ground truth labels, making them suitable for unsupervised settings. On the other hand, ARI and NMI are more pertinent when ground truth labels are available. Additionally, visual inspection through methods like PCA or t-SNE can provide an intuitive sense of the cluster configuration, complementing numerical metrics.

While using these metrics, it’s essential to remember that no single evaluation metric can capture every aspect of clustering quality. Typically, a combination of intrinsic and extrinsic metrics, along with visual inspection, provides a more comprehensive validation of clustering performance.

Real-world Clustering Examples and Case Studies

In the realm of real-world applications, clustering algorithms serve as indispensable tools across various domains in data science and beyond. Below we delve into concrete case studies and examples where clustering techniques have demonstrated their efficacy.

Customer Segmentation in Retail

Customer segmentation is a quintessential application of clustering in the retail industry. Retailers utilize clustering methods like K-means to identify distinct customer groups based on purchasing behavior, demographics, or browsing history. For instance, a retailer could segment its customer base into categories such as “bargain hunters,” “loyal buyers,” and “seasonal shoppers.” This enables targeted marketing strategies and personalized communication, ultimately boosting sales and customer satisfaction.

Example with Python and K-Means:

from sklearn.cluster import KMeans
import pandas as pd

# Sample data
data = {'CustomerID': [1, 2, 3, 4, 5],
        'AnnualIncome': [15000, 50000, 35000, 80000, 45000],
        'SpendingScore': [20, 60, 50, 80, 55]}

df = pd.DataFrame(data)

# Applying K-Means
kmeans = KMeans(n_clusters=2)
df['Cluster'] = kmeans.fit_predict(df[['AnnualIncome', 'SpendingScore']])

print(df)

Anomaly Detection in Network Security

In cybersecurity, clustering algorithms like DBSCAN (Density-Based Spatial Clustering of Applications with Noise) are employed to detect anomalies. By identifying outliers in network traffic data, security systems can pinpoint potential malicious activities or breaches. DBSCAN’s ability to form clusters of arbitrary shape and ignore noise makes it particularly suitable for this purpose.

Example with Python and DBSCAN:

from sklearn.cluster import DBSCAN
import numpy as np

# Sample network traffic data
data = np.array([[1, 2], [2, 2], [2, 3], [8, 7], [8, 8], [25, 80]])

# Applying DBSCAN
dbscan = DBSCAN(eps=3, min_samples=2)
clusters = dbscan.fit_predict(data)

print(clusters)

Image Segmentation in Medical Imaging

In medical imaging, clustering is pivotal for tasks such as segmenting different tissues, organs, or pathologies from medical scans. Hierarchical clustering, among other methods, is utilized to differentiate between various regions in MRI or CT scans, aiding in the diagnosis and treatment planning for diseases like cancer.

Example with Python and Hierarchical Clustering:

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt

# Sample image data (flattened for simplicity)
data = np.array([[1.0, 1.1], [1.5, 1.6], [3.0, 3.3], [5.0, 5.1], [3.5, 3.6]])

# Applying Hierarchical Clustering
linkage_matrix = linkage(data, 'ward')
dendrogram(linkage_matrix)
plt.show()

Market Basket Analysis in E-Commerce

E-commerce platforms often employ clustering techniques for market basket analysis. By clustering items frequently bought together, businesses can optimize cross-selling strategies and improve the recommendation systems. This enhances the user experience and directly impacts sales.

Example with Python and Agglomerative Clustering:

from sklearn.cluster import AgglomerativeClustering
import numpy as np

# Sample transaction data
data = np.array([[0, 1, 1, 0], [1, 1, 0, 0], [0, 1, 1, 1], [1, 0, 0, 1]])

# Applying Agglomerative Clustering
agglo_cluster = AgglomerativeClustering(n_clusters=2)
clusters = agglo_cluster.fit_predict(data)

print(clusters)

Document Clustering in News Aggregation

In the domain of news aggregation, clustering is used to group articles into topics or themes. This allows for better organization and navigation of content. Algorithms like Latent Dirichlet Allocation (LDA) often work in tandem with clustering methods to refine the groupings.

Example with Python and LDA followed by Clustering:

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation
from sklearn.cluster import KMeans

# Sample document data
documents = ["The cat sat on the mat.", "Dogs are great pets.", "Cats and dogs play together."]

# Vectorizing the text data
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(documents)

# Applying LDA
lda = LatentDirichletAllocation(n_components=2)
X_topics = lda.fit_transform(X)

# Clustering the topics
kmeans = KMeans(n_clusters=2)
clusters = kmeans.fit_predict(X_topics)

print(clusters)

These examples highlight the versatility and power of clustering algorithms in extracting meaningful patterns and groups from data, providing invaluable insights and driving numerous applications across diverse fields.