Code Vibes

neural network, artificial neural network, human brain

Mastering Logistic Regression for Classification Problems

Sophia Johnson

Welcome to our comprehensive guide on mastering Logistic Regression for classification problems. In this article, we will demystify the Logistic Regression algorithm and explore its applications in machine learning classification tasks. Whether you’re a beginner looking to understand the basics or an advanced practitioner seeking to refine your skills, this detailed Logistic Regression tutorial is designed to guide you through the intricate workings and powerful capabilities of this foundational statistical tool. By the end, you’ll have a robust understanding of how to build, interpret, and optimize a Logistic Regression model for accurate and efficient classification. Let’s dive in and start our journey toward mastering Logistic Regression!

Introduction to Logistic Regression

Introduction to Logistic Regression

Logistic Regression, despite its name, is a foundational machine learning classification algorithm used to predict binary outcomes. Its primary objective is to model the relationship between a dependent binary variable and one or more independent variables. Unlike linear regression, which predicts continuous outcomes, logistic regression predicts probabilities constrained between 0 and 1, making it well-suited to classification tasks.

The core of logistic regression lies in its sigmoid function, also known as the logistic function. The sigmoid function maps any real-valued number into a value between 0 and 1. This function is particularly useful for binary classification since it allows for a probabilistic interpretation of the output. Specifically, the logistic function is defined as:

    \[ \sigma(z) = \frac{1}{1 + e^{-z}} \]

Here, ( z ) represents the linear combination of the input features:

    \[ z = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n \]

Where:

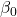  • \beta_0 is the intercept term,
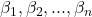  • \beta_1, \beta_2, ..., \beta_n are the coefficients,
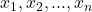  • x_1, x_2, ..., x_n are the feature values.

The output of the sigmoid function, \sigma(z), provides the probability of the dependent variable y being equal to 1 for binary classification (e.g., spam vs. not spam, disease vs. healthy). If the probability exceeds a chosen threshold (commonly 0.5), the instance is classified into the positive class; otherwise, it is classified into the negative class.

To illustrate, consider a simple binary classification problem where we want to predict whether an email is spam (1) or not spam (0) based on features like word frequency. By applying logistic regression, we can estimate the probability that given an email is spam and use this probability to make our classification decision.

Python’s popular libraries such as scikit-learn make it straightforward to implement logistic regression. Here is a basic example using scikit-learn:

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# Load dataset
iris = load_iris()
X = iris.data[iris.target != 2]
y = iris.target[iris.target != 2]

# Split dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create a logistic regression model
model = LogisticRegression()

# Train the model
model.fit(X_train, y_train)

# Predict on test data
y_pred = model.predict(X_test)

# Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
print(f"Model Accuracy: {accuracy}")

In this code snippet, we use a simple dataset (the Iris dataset, limited to a binary classification problem for simplicity), split it into training and testing sets, and train a logistic regression model. The model’s performance is evaluated based on its accuracy in predicting the test data.

In conclusion, logistic regression is a powerful tool in the machine learning toolbox for binary classification problems. Its ease of interpretation and probabilistic nature make it accessible and understandable, even for large and complex datasets. For more detailed information on logistic regression, refer to scikit-learn’s official documentation.

Mathematical Foundations of the Logistic Regression Algorithm

The logistic regression algorithm functions on the foundational principles of probability theory and linear algebra. Unlike linear regression, which is suited for predicting continuous outcomes, logistic regression targets binary outcomes. This is particularly useful for classification tasks where the output is categorical, such as spam detection, medical diagnosis, and sentiment analysis.

At its core, logistic regression estimates the probability that a given input falls into a specific class. The model uses the logistic function, also known as the sigmoid function, to map predicted values to probabilities. Mathematically, the logistic function is defined as:

    \[ h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx}} \]

Where:

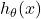  • h_\theta(x) is the predicted probability.
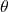  • \theta are the model parameters (weights).
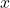  • x is the input feature vector.
  • e is the base of the natural logarithm.

Linear Combination of Inputs

The linear combination of the input features and their corresponding weights is calculated as \theta^T x, where \theta^T indicates the transpose of the parameter vector \theta. For example, if you have three features x_1, x_2, and x_3, this combination will look like:

    \[ \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 \]

Sigmoid Activation

The sigmoid activation function transforms the linear combination into a probability:

    \[ \sigma(z) = \frac{1}{1 + e^{-z}} \]

In logistic regression, z = \theta^T x. This function outputs a value between 0 and 1, which can be interpreted as a probability. For a decision boundary, usually, a threshold of 0.5 is used. If h_\theta(x) \geq 0.5, the prediction is class 1; otherwise, the prediction is class 0.

Loss Function

To train the logistic regression model, we optimize the parameters \theta to minimize the loss function, specifically the binary cross-entropy loss (also known as log loss). The loss function for a single training example can be defined as:

    \[ \text{Loss}(h_\theta(x), y) = - [y \log(h_\theta(x)) + (1 - y) \log(1 - h_\theta(x))] \]

Where:

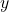  • y is the actual label (0 or 1).
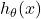  • h_\theta(x) is the predicted probability.

The loss is minimized across all training examples to find the optimal parameters:

    \[ J(\theta) = -\frac{1}{m} \sum_{i=1}^m [y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)}))] \]

Where:

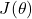  • J(\theta) is the cost function.
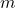  • m is the number of training examples.

Gradient Descent

To minimize the cost function ( J(\theta) ), we use an iterative optimization algorithm called gradient descent. The gradients of the cost function with respect to each parameter \theta_j are computed as:

    \[ \frac{\partial J(\theta)}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} \]

The parameters are updated using these gradients:

    \[ \theta_j := \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j} \]

Where \alpha is the learning rate, which controls how big a step is taken in the direction of the gradient.

Regularization

To prevent overfitting, logistic regression models can be regularized. Two common regularization techniques are L1 (Lasso) and L2 (Ridge) regularization. The regularized cost function for L2 regularization (Ridge) is:

    \[ J(\theta) = -\frac{1}{m} \sum_{i=1}^m [y^{(i)} \log(h_\theta(x^{(i)(})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)}))] + \frac{\lambda}{2m} \sum_{j=1}^n \theta_j^2 \]

Where \lambda is the regularization parameter that controls the amount of shrinkage applied to the coefficients.

For further details on the mathematical foundations of the logistic regression algorithm, refer to the comprehensive documentation and resources on Scikit-learn’s Logistic Regression and the Deep Learning Book.

Building and Training Logistic Regression Models

Building and Training Logistic Regression Models

To effectively leverage logistic regression for classification problems, one must master the process of building and training logistic regression models. Here, we’ll delve into the practical steps and best practices suitable for a robust implementation.

Data Preparation

The cornerstone of building any machine learning model is meticulous data preparation. Begin by importing and cleansing your dataset. Ensure any missing values are handled appropriately; options include imputation or exclusion of such data points. Also, standardize or normalize the features if they vary drastically in magnitude.

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# Example data loading
data = pd.read_csv('your_dataset.csv')
X = data.drop(columns='target')
y = data['target']

# Handling missing values
X.fillna(X.mean(), inplace=True)

# Split into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Feature scaling
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Model Selection and Initialization

The next step is initializing the logistic regression model. Scikit-learn offers a highly configurable LogisticRegression class suited for various logistic regression techniques.

from sklearn.linear_model import LogisticRegression

# Initialize logistic regression model
logistic_regression_model = LogisticRegression(max_iter=1000, random_state=42)

Key Parameters to Consider:

  • Penalty (Regularization): Choose ‘l1’ for Lasso, ‘l2’ for Ridge, or ‘elasticnet’ for combining both.
  • C (Inverse of Regularization Strength): Smaller values signify stronger regularization.
  • Solver: Each solver (liblinear, newton-cg, lbfgs, saga) is optimized for particular datasets and should be chosen based on the feature space and dataset size.

Training the Model

Training the model involves fitting it to your dataset. This step tunes the model’s parameters to best fit the data, enabling it to learn the relationship between features and the target variable.

# Fit the model to training data
logistic_regression_model.fit(X_train, y_train)

Hyperparameter Tuning

Hyperparameters drastically affect the model’s performance. Utilizing techniques like Grid Search or Random Search can help in finding the best combination of hyperparameters for your logistic regression model.

from sklearn.model_selection import GridSearchCV

# Define hyperparameters and their values
param_grid = {
    'penalty': ['l1', 'l2'],
    'C': [0.01, 0.1, 1, 10],
    'solver': ['liblinear', 'saga']
}

# Initialize grid search
grid_search = GridSearchCV(estimator=logistic_regression_model, param_grid=param_grid, cv=5, verbose=1, n_jobs=-1)

# Perform grid search
grid_search.fit(X_train, y_train)

# Output best parameters
print("Best Parameters: ", grid_search.best_params_)

Model Evaluation

After training, evaluate the model’s performance on the test dataset. Scikit-learn offers various metrics such as accuracy, precision, recall, and F1-score to measure the effectiveness of your logistic regression model.

from sklearn.metrics import classification_report, accuracy_score

# Predict the class labels for the test set
y_pred = grid_search.best_estimator_.predict(X_test)

# Evaluate the model
print("Accuracy: ", accuracy_score(y_test, y_pred))
print(classification_report(y_test, y_pred))

Pros and Cons of Logistic Regression

While logistic regression is excellent for binary classification problems due to its simplicity and interpretability, it has certain limitations. It assumes a linear relationship between the features and the log odds of the outcome, which may not always capture the complexity of real-world data. Regularization techniques such as Ridge (L2) and Lasso (L1) help mitigate overfitting but may require extensive experimentation.

Refer to the official sklearn documentation for an exhaustive list of configurable parameters and additional customization options.

By carefully preparing your data, selecting the appropriate model configurations, and tuning hyperparameters, you can build efficient and effective logistic regression models tailored to your specific classification problem.

Logistic Regression Techniques for Classification

One of the key aspects of mastering logistic regression for classification problems is understanding and leveraging various logistic regression techniques. These techniques can greatly enhance the model’s performance, interpretability, and efficiency in predictive tasks.

Feature Engineering

Effective feature engineering is fundamental when working with logistic regression models. This involves creating new features from the data, normalizing or standardizing features to improve model convergence, and handling categorical variables appropriately. For instance, categorical variables can be encoded using techniques like One-Hot Encoding or using polynomial transformations for more complex relationships.

from sklearn.preprocessing import OneHotEncoder, StandardScaler

# Example dataset
data = [
    {'age': 29, 'income': 72000, 'city': 'New York'},
    {'age': 52, 'income': 54000, 'city': 'San Francisco'},
    {'age': 37, 'income': 91000, 'city': 'Los Angeles'}
]

# One-Hot Encoding for categorical 'city' feature
encoder = OneHotEncoder()
city_encoded = encoder.fit_transform([d['city'] for d in data])

# Standardizing numerical features
scaler = StandardScaler()
scaled_features = scaler.fit_transform([[d['age'], d['income']] for d in data])

Regularization Techniques

Logistic regression can suffer from overfitting, particularly when the number of features is large. Regularization techniques such as L1 (Lasso) and L2 (Ridge) regularization help mitigate this by adding penalty terms to the loss function. The choice between L1 and L2 regularization depends on the specific use case: L1 can induce sparsity in the model (useful for feature selection), while L2 distributes the penalty more smoothly across all coefficients.

from sklearn.linear_model import LogisticRegression

# L1 Regularization
model_l1 = LogisticRegression(penalty='l1', solver='liblinear')
model_l1.fit(X_train, y_train)

# L2 Regularization
model_l2 = LogisticRegression(penalty='l2')
model_l2.fit(X_train, y_train)

Feature Selection

Feature selection is often used to identify the most important variables, simplifying models and improving performance. Techniques include Recursive Feature Elimination (RFE), where features are recursively pruned, and selecting features based on model coefficients’ magnitudes.

from sklearn.feature_selection import RFE

# Recursive Feature Elimination
rfe = RFE(estimator=LogisticRegression(), n_features_to_select=5)
rfe.fit(X_train, y_train)
selected_features = rfe.support_

Handling Imbalanced Data

Classification problems often involve imbalanced datasets where one class is underrepresented. Logistic regression models can be biased towards the majority class. Techniques like Synthetic Minority Over-sampling Technique (SMOTE), adjusting class weights, or undersampling the majority class can be employed to address this issue.

from imblearn.over_sampling import SMOTE

smote = SMOTE(sampling_strategy='minority')
X_resampled, y_resampled = smote.fit_resample(X_train, y_train)

Hyperparameter Tuning

Tuning hyperparameters, such as the regularization strength (C parameter), can significantly affect the performance of logistic regression models. Grid Search and Random Search are common techniques for hyperparameter optimization.

from sklearn.model_selection import GridSearchCV

# Grid Search for hyperparameter tuning
param_grid = {'C': [0.01, 0.1, 1, 10, 100]}
grid_search = GridSearchCV(LogisticRegression(), param_grid, cv=5)
grid_search.fit(X_train, y_train)
best_params = grid_search.best_params_

Model Interpretation

Understanding the coefficients’ contribution to the model’s predictions is crucial for interpretability. In logistic regression, coefficients can be converted to odds ratios, providing a more intuitive understanding of the model.

import numpy as np

# Model coefficients to odds ratios
model = LogisticRegression()
model.fit(X_train, y_train)
odds_ratios = np.exp(model.coef_)

By applying these logistic regression techniques, one can build robust models that are better suited to tackle complex classification problems. For more detailed information, refer to the Scikit-Learn documentation on logistic regression.

Evaluating and Interpreting Logistic Regression Models

Evaluating and interpreting logistic regression models is essential to ensure that your model accurately predicts the binary outcome and provides insights into the underlying relationships between variables. This section will cover various methods and metrics for assessing the performance and correctness of your logistic regression model.

Performance Metrics

Accuracy

Accuracy is one of the simplest metrics to evaluate the performance of a logistic regression model. It is the ratio of correctly predicted instances to the total instances. However, accuracy may not be the best metric, particularly if you have imbalanced datasets, where the classes are not equally represented.

from sklearn.metrics import accuracy_score

# Assuming y_test and y_pred are the true and predicted labels, respectively
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')

Precision, Recall, and F1-Score

Precision (Positive Predictive Value) and Recall (Sensitivity or True Positive Rate) are more informative metrics when dealing with imbalanced classes. Precision tells you what proportion of predicted positives was actually positive, whereas Recall tells you what proportion of actual positives was correctly identified by the model. The F1-Score is the harmonic mean of Precision and Recall, providing a balance between the two metrics.

from sklearn.metrics import precision_score, recall_score, f1_score

precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)

print(f'Precision: {precision:.2f}')
print(f'Recall: {recall:.2f}')
print(f'F1-Score: {f1:.2f}')

ROC Curve and AUC

The Receiver Operating Characteristic (ROC) curve plots the True Positive Rate against the False Positive Rate at various threshold settings, providing a visual representation of the trade-offs between sensitivity and specificity. The Area Under the ROC Curve (AUC) quantifies this trade-off and provides a single metric, where an AUC of 1.0 represents a perfect model.

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt

# Calculate the probabilities
y_prob = model.predict_proba(X_test)[:, 1]

# Compute ROC curve and AUC score
fpr, tpr, _ = roc_curve(y_test, y_prob)
roc_auc = roc_auc_score(y_test, y_prob)

# Plot ROC curve
plt.figure()
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='red', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc="lower right")
plt.show()

print(f'ROC AUC: {roc_auc:.2f}')

Interpreting Coefficients

The coefficients in a logistic regression model represent the log odds changes in the dependent variable for each unit increase in the predictor variable. To interpret these coefficients, you can exponentiate them to obtain the odds ratios, which are more intuitive.

import numpy as np

# Assuming `model` is your trained logistic regression model
coefficients = model.coef_[0]
odds_ratios = np.exp(coefficients)

for feature, odds_ratio in zip(feature_names, odds_ratios):
    print(f'{feature}: {odds_ratio:.2f}')

Checking for Multicollinearity

Multicollinearity can affect the stability and interpretation of logistic regression coefficients. Variance Inflation Factor (VIF) is a common method to diagnose multicollinearity. A VIF value greater than 10 indicates significant multicollinearity.

from statsmodels.stats.outliers_influence import variance_inflation_factor
import pandas as pd

# Assuming X_train is your feature DataFrame
vif_data = pd.DataFrame()
vif_data['Feature'] = X_train.columns
vif_data['VIF'] = [variance_inflation_factor(X_train.values, i) for i in range(X_train.shape[1])]

print(vif_data)

Checking Assumptions and Diagnostics

  • Linearity of the Logit: Ensure that the logit transformation has a linear relationship with the independent variables.
  • Absence of Perfect Multicollinearity: Check for VIF to diagnose multicollinearity.
  • Independence of Errors: Ensure that the residuals are independent.
import statsmodels.api as sm

# Assuming X_train and y_train are your features and target
logit_model = sm.Logit(y_train, X_train)
result = logit_model.fit()
print(result.summary())

By using these metrics and diagnostic checks, you can evaluate the robustness and performance of your logistic regression model, ensuring it achieves the desired predictive power and interpretability. For further reading, you can explore the scikit-learn documentation and statsmodels user guide.

Advanced Logistic Regression Methods and Tips

When it comes to advanced logistic regression methods, understanding these nuances can significantly elevate your modeling capabilities. Here are several advanced techniques and tips for optimizing your logistic regression model, ensuring robustness and efficiency.

Feature Engineering and Selection

One key aspect of improving logistic regression models is through effective feature engineering. Creating meaningful features that capture underlying patterns in your data can greatly enhance model performance. Additionally, feature selection is crucial for eliminating irrelevant variables which can otherwise introduce noise and lead to overfitting. Techniques like Recursive Feature Elimination (RFE) and regularization methods such as Lasso (L1 regularization) can be beneficial.

Example using RFE:

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
rfe = RFE(model, 5)
fit = rfe.fit(X_train, y_train)
print("Num Features: %s" % (fit.n_features_))
print("Selected Features: %s" % (fit.support_))
print("Feature Ranking: %s" % (fit.ranking_))

Regularization Techniques

Regularization is a method to prevent overfitting by penalizing large coefficients in the logistic regression algorithm. There are primarily two types of regularization techniques used in logistic regression:

  1. Lasso Regression (L1 regularization):
    L1 regularization can shrink some parameters to zero, performing variable selection inherently.

    from sklearn.linear_model import LogisticRegression

lasso_model = LogisticRegression(penalty='l1', solver='saga')
lasso_model.fit(X_train, y_train)
  2. Ridge Regression (L2 regularization):
    L2 regularization can shrink coefficients but not zero them out, keeping all features but reducing their influence.

    ridge_model = LogisticRegression(penalty='l2')
ridge_model.fit(X_train, y_train)

Hyperparameter Tuning

Optimization of hyperparameters can drastically improve the logistic regression model’s performance. Use techniques like Grid Search or Random Search to find the best configurations for your model.

Example using Grid Search:

from sklearn.model_selection import GridSearchCV

param_grid = {'C': [0.1, 1, 10, 100], 'penalty': ['l1', 'l2']}
grid_model = GridSearchCV(LogisticRegression(solver='saga'), param_grid, cv=5, scoring='accuracy')
grid_model.fit(X_train, y_train)
print("Best Parameters: ", grid_model.best_params_)

Addressing Imbalanced Datasets

In many practical scenarios, especially in classification problems, the dataset may be highly imbalanced. Techniques such as Stratified Sampling, SMOTE (Synthetic Minority Over-sampling Technique), and adjusting class weights can help to mitigate this challenge.

Example using SMOTE:

from imblearn.over_sampling import SMOTE

sm = SMOTE(random_state=42)
X_res, y_res = sm.fit_resample(X_train, y_train)

Model Validation

Cross-validation helps in assessing the model’s performance on different subsets of the data, providing a more reliable estimate of the model’s generalization ability. K-Fold Cross Validation is commonly used for this purpose.

Example using K-Fold Cross-Validation:

from sklearn.model_selection import cross_val_score

model = LogisticRegression(penalty='l2')
scores = cross_val_score(model, X_train, y_train, cv=10, scoring='accuracy')
print("Cross-validated scores: ", scores)

Incorporating Interaction Terms

Sometimes, the relationship between predictors can be complex, and incorporating interaction terms could reveal hidden interactions between variables that a model with only linear terms might miss.

Example including interaction terms using PolynomialFeatures:

from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(interaction_only=True, include_bias=False)
X_train_interactions = poly.fit_transform(X_train)

By leveraging these advanced techniques and tips, you can optimize and fine-tune your logistic regression models for a variety of classification problems. Visit the scikit-learn documentation for detailed information and further reading on logistic regression.

Practical Applications: Logistic Regression Examples

In this section, we will focus on practical applications to help you understand how to apply logistic regression in real-world classification scenarios. By the end, you should have a clear sense of where Logistic Regression can be applied effectively. Let’s delve into some classic examples that exploit the capabilities of this powerful statistical method.

1. Medical Diagnosis

One of the most popular applications of the Logistic Regression algorithm is in the field of medical diagnosis. For instance, predicting whether a patient has a particular disease based on various diagnostic tests is a common use case.

Example: Predicting Diabetes

  • Dataset: One commonly used dataset is the Pima Indians Diabetes Database. This dataset contains medical records with attributes such as age, blood pressure, BMI, and the test results of diabetes (positive or negative).
  • Implementation:
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report

# Load the dataset
data = pd.read_csv('pima-indians-diabetes.csv')
X = data.drop('Outcome', axis=1)
y = data['Outcome']

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize and train the model
model = LogisticRegression()
model.fit(X_train, y_train)

# Predictions
y_pred = model.predict(X_test)

# Evaluation
print(classification_report(y_test, y_pred))

2. Email Spam Detection

Logistic Regression is often used to classify emails as spam or not spam. Attributes for the logistic regression model can include the presence of certain keywords, the sender’s email address, and the email’s metadata.

Example: Predicting Spam Emails

  • Dataset: SpamAssassin Public Corpus is a good dataset containing spam and non-spam emails.
  • Implementation Approach: Extract features from emails using techniques like TF-IDF (Term Frequency-Inverse Document Frequency) and then fit these features into a logistic regression model.
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load data
emails, labels = load_spam_dataset()  # Assume a function that loads emails and labels

# Feature extraction
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(emails)
y = labels

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize and train the model
model = LogisticRegression()
model.fit(X_train, y_train)

# Predictions
y_pred = model.predict(X_test)

# Evaluation
print("Accuracy:", accuracy_score(y_test, y_pred))

3. Customer Churn Prediction

Organizations often use logistic regression to predict customer churn, i.e., which customers are likely to stop using a service based on their behavior and demographics.

Example: Predicting Customer Churn

  • Dataset: Telecommunications, subscription services, and online platforms often collect data conducive to churn analysis.
  • Implementation:
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score

# Load sample dataset
data = pd.read_csv('telecom_churn.csv')
X = data.drop('Churn', axis=1)
y = data['Churn']

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize and train the model
model = LogisticRegression()
model.fit(X_train, y_train)

# Predictions
y_pred_prob = model.predict_proba(X_test)[:, 1]

# Evaluation
print("ROC AUC Score:", roc_auc_score(y_test, y_pred_prob))

These examples illustrate how logistic regression is applied across various domains. Each application makes use of logistic regression’s ability to model the probability of different categorical outcomes clearly and effectively. Moreover, these scenarios provide concrete code snippets that you can adapt to your specific needs, paving the way for you to master this fundamental machine learning classification technique. For more advanced uses and techniques related to Logistic Regression, visit the official scikit-learn documentation.

Related Posts