In the rapidly evolving field of artificial intelligence and machine learning, ensuring the robustness and accuracy of models is paramount. One of the most critical challenges faced by data scientists and AI practitioners is overfitting, where a model performs well on training data but fails to generalize to unseen datasets. To address this issue, a variety of regularization techniques have been developed. This article delves into the various strategies, including L1 and L2 regularization, Ridge and Lasso regression, and other advanced methods like dropout and weight decay, all aimed at enhancing AI performance and preventing overfitting. Read on to discover the essential tools for optimizing your AI models and achieving better model generalization.

Understanding Overfitting in AI Models

Overfitting is a common problem that occurs when an AI model learns the details and noise in the training data to the extent that it negatively impacts the model’s performance on new data. This means the model performs well on the training dataset but fails to generalize to unseen data, manifesting in poor predictive capabilities when applied to test datasets or real-world scenarios.

Identifying Overfitting

One primary indicator of overfitting is observing a significant disparity in performance metrics, such as accuracy or loss, between the training and validation/test datasets. Typically, an overfitting model will exhibit substantially higher accuracy on training data but significantly lower accuracy on validation data.

Causes of Overfitting

1. Complex Models: Powerful models, especially with many parameters like deep neural networks, can capture intricate patterns—even noise—in the training data.
2. Insufficient Training Data: Limited data points can make a model overly sensitive to small fluctuations in the training set, rather than learning the underlying trends.
3. Noisy Data: Presence of noise and outliers in the data can lead to overfitting as the model might fit to these imperfections.
4. Excessive Features: Having a high number of features relative to the number of observations can also make the model prone to overfitting.

Visualizing Overfitting

A visual representation can often make it clearer. Consider a simple polynomial regression example:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# Generate some data
np.random.seed(0)
X = np.linspace(0, 1, 15).reshape(-1, 1)
y = np.sin(2 * np.pi * X).ravel() + np.random.normal(scale=0.1, size=15)

# Fit a very high-degree polynomial model
poly = PolynomialFeatures(degree=15)
X_poly = poly.fit_transform(X)
model = LinearRegression()
model.fit(X_poly, y)

# Predict values
X_test = np.linspace(0, 1, 100).reshape(-1, 1)
X_test_poly = poly.transform(X_test)
y_pred = model.predict(X_test_poly)

# Plot the results
plt.scatter(X, y, color='black', label='Data')
plt.plot(X_test, y_pred, color='red', label='Model')
plt.legend()
plt.show()

In the above example, the regression model fits exceptionally well to the training data points but produces a highly oscillatory and non-generalizable curve, typifying overfitting.

Mathematical Formulation

In mathematical terms, overfitting can be formalized in the bias-variance tradeoff framework. Consider a model’s error decomposed into three parts:

• Bias: Error due to overly simplistic assumptions in the model.
• Variance: Error due to sensitivity to small fluctuations in the training data.
• Irreducible Error: Error inherent in the data itself.

Overfitting results in low bias but high variance, where the model learns the minutiae of the training data and fails to generalize.

Diagnosing Overfitting with Metrics

Common metrics to diagnose and quantify overfitting include:

• Training vs. Validation Error: Significant difference typically indicates overfitting.
• Learning Curves: Plotting the training and validation errors over epochs can help visualize the point where the model starts overfitting.

from sklearn.model_selection import learning_curve

# Assuming model and data (X, y) are defined
train_sizes, train_scores, validation_scores = learning_curve(
    estimator=model, X=X, y=y, train_sizes=np.linspace(0.1, 1.0, 50), cv=5,
    scoring='neg_mean_squared_error'
)

train_scores_mean = -train_scores.mean(axis=1)
validation_scores_mean = -validation_scores.mean(axis=1)

plt.plot(train_sizes, train_scores_mean, label='Training error')
plt.plot(train_sizes, validation_scores_mean, label='Validation error')
plt.ylabel('MSE')
plt.xlabel('Training size')
plt.legend()
plt.show()

This plot will show how errors evolve with training size and can highlight the stage where validation error starts increasing while training error keeps decreasing, signaling overfitting.

Understanding the mechanism and implications of overfitting is crucial for developing robust AI models, laying the groundwork for the strategic application of regularization techniques.

Introduction to Regularization Methods in Machine Learning

In the realm of machine learning, one of the core challenges when developing AI models is ensuring they generalize well to new, unseen data. This is where regularization methods come into play. Regularization techniques are crucial tools in the data scientist’s toolkit, designed to prevent overfitting by adding a penalty to the model for complexity. These penalties constrain the optimization function, thus simplifying the model and improving its ability to generalize.

Regularization Techniques Overview

At the heart of regularization lies the principle of bias-variance tradeoff. These techniques aim to strike a balance between fitting the training data (low bias) and maintaining the model’s ability to generalize on new data (low variance). There are several popular regularization methods each with its unique advantages and applications.

L1 Regularization (Lasso)

L1 regularization, also known as Lasso (Least Absolute Shrinkage and Selection Operator), introduces a penalty equal to the absolute value of the magnitude of coefficients. It effectively shrinks some coefficients to zero, thus performing feature selection. This is particularly useful in high-dimensional data scenarios where interpreting model coefficients is crucial.

from sklearn.linear_model import Lasso

# Example usage
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)
predictions = lasso.predict(X_test)

For further details, check the Lasso documentation on scikit-learn.

L2 Regularization (Ridge)

L2 regularization, or Ridge regression, adds a penalty equal to the square of the magnitude of coefficients. Unlike Lasso, Ridge doesn’t set coefficients to zero but rather penalizes large coefficients more heavily, which leads to smaller, spread-out values. This is useful when all features might be of significance but need to be regularized to prevent overfitting.

from sklearn.linear_model import Ridge

# Example usage
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)
predictions = ridge.predict(X_test)

Refer to the Ridge regression documentation on scikit-learn for additional information.

Dropout in Neural Networks

For deep learning applications, Dropout is a popular technique to prevent overfitting. It involves randomly dropping units (neurons) from the neural network during training, which forces the network to learn robust features that are distributed and less reliant on specific neurons.

import tensorflow as tf
from tensorflow.keras.layers import Dropout

# Example usage within a neural network
model = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    Dropout(0.5),
    tf.keras.layers.Dense(units=10, activation='softmax')
])

model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=10, validation_split=0.2)

Explore more in the TensorFlow guide on Dropout.

Cross-Validation

Cross-validation is another critical method that works hand-in-hand with regularization to prevent overfitting. By repeatedly dividing the data into training and validation sets, cross-validation ensures the model’s performance is consistent across different subsets of data.

from sklearn.model_selection import cross_val_score

# Example usage
model = Ridge(alpha=1.0)
scores = cross_val_score(model, X, y, cv=10)

Reference the scikit-learn cross-validation documentation for more comprehensive guidelines.

Combining Regularization Methods

Often, data scientists combine multiple regularization techniques to achieve significant gains in AI performance. For example, using L2 regularization along with dropout can be an effective strategy in training robust neural networks. Perfecting these combinations requires fine-tuning regularization strength and neural network architecture based on the problem domain and data characteristics.

Adopting a systematic approach to regularization allows you to build AI models that perform well under various scenarios, ensuring better generalization capabilities and higher robustness against overfitting.

L1 Regularization (Lasso Regression) and Its Applications

L1 Regularization, also known as Lasso Regression (Least Absolute Shrinkage and Selection Operator), is a popular technique utilized to enhance the performance of AI models by mitigating overfitting. At its core, Lasso regression incorporates a penalty term to the loss function based on the absolute values of the coefficients. This can be expressed mathematically as follows:

Here, is the regularization parameter that determines the weight of the penalty term, and are the model coefficients. By adding this penalty term, Lasso encourages the coefficients of less significant features to shrink towards zero, thus performing both regularization and feature selection.

Applications of Lasso Regression

1. Feature Selection:
   Lasso regression is particularly useful when dealing with datasets that have numerous features. By zeroing out the less important features, it effectively reduces the dimensionality of the model. This is not just beneficial for improving model performance, but it also enhances the interpretability by isolating impactful features.

   from sklearn.linear_model import Lasso
   
   # Example dataset
   X, y = load_some_data()
   
   # Initialize Lasso with an alpha of 0.1
   lasso = Lasso(alpha=0.1)
   lasso.fit(X, y)
   
   # Get coefficients
   print(lasso.coef_)
   

2. Sparse Data:
   In cases where the dataset is sparse, L1 regularization can be exceptionally advantageous. The sparsity-inducing property of Lasso makes it suitable for problems like text classification and bioinformatics where datasets often contain a large number of zero entries.
3. Interpretable Machine Learning Models:
   Due to its inherent feature selection characteristic, Lasso models are simpler and often easier to interpret compared to other regression models. These interpretable models are crucial in fields such as healthcare and finance, where understanding the influence of each predictor is essential.

Examples in Different Domains

• Finance:
  Lasso regression is widely used for credit scoring and risk analysis. By selecting the most relevant financial indicators, Lasso helps in creating robust predictive models that can effectively identify potential defaulters.
• Bioinformatics:
  In genetic studies, Lasso regression aids in pinpointing the specific genes that are predictive of a disease, thereby facilitating a better understanding of the underlying genetic factors.
• Marketing:
  Lasso regression can optimize marketing campaigns by determining which customer features (e.g., age, income, past purchases) significantly influence the probability of a purchase.

Hyperparameter Tuning and Model Evaluation

To achieve optimal performance from a Lasso model, it’s crucial to tune the parameter carefully. This can be accomplished using cross-validation techniques:

from sklearn.model_selection import GridSearchCV

# Define the alpha parameter grid
param_grid = {'alpha': [0.01, 0.1, 1, 10, 100]}

# Initialize Lasso
lasso = Lasso()

# Set up the grid search with cross-validation
grid_search = GridSearchCV(lasso, param_grid, cv=5)
grid_search.fit(X, y)

# Best parameter and corresponding score
print(grid_search.best_params_)
print(grid_search.best_score_)

L1 regularization, or Lasso regression, stands out as a versatile and powerful tool in the arsenal of regularization techniques. Its ability to streamline models by zeroing out non-essential features ensures not just enhanced AI performance but also greater model interpretability, catering to the diverse needs of data science and machine learning applications.

L2 Regularization (Ridge Regression) and Benefits

L2 Regularization, often referred to as Ridge Regression, is a widely-used technique in machine learning for preventing overfitting by penalizing the magnitude of the model coefficients. It does this by adding a penalty equivalent to the square of the magnitude of coefficients to the loss function. The regularization term added to the loss function is given by:

where is the regularization parameter, represents the model parameters, and is the number of parameters.

The key benefit of L2 regularization is that it discourages the model from relying too heavily on any one feature, which in turn helps to prevent overfitting. This is particularly effective in high-dimensional spaces where the number of features exceeds the number of observations.

Implementation Example:

In Python, L2 regularization can be implemented using libraries such as Scikit-Learn. Here is a basic implementation of Ridge Regression with Scikit-Learn:

from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn import datasets

# Load dataset
data = datasets.load_boston()
X = data.data
y = data.target

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize Ridge Regression with a chosen alpha parameter (regularization strength)
ridge_reg = Ridge(alpha=1.0)

# Fit the model
ridge_reg.fit(X_train, y_train)

# Predict
predictions = ridge_reg.predict(X_test)

In this example, serves as , controlling the regularization strength. A higher value of will impose a larger penalty on the coefficients, potentially leading to even smaller fitted coefficients.

Advantages of L2 Regularization:

1. Improves Model Generalization:
   By penalizing large coefficients, Ridge Regression ensures that the model does not overly depend on any single feature, improving the model’s ability to generalize to unseen data.
2. Reduces Multicollinearity:
   In datasets with highly correlated features, Ridge Regression can reduce the variance among the correlated variables, effectively dealing with multicollinearity.
3. Computational Efficiency:
   Compared to L1 Regularization (Lasso Regression), Ridge tends to be more computationally stable and efficient, especially with high-dimensional datasets where the number of features is very large.
4. Solves Singular Matrix Issue:
   In linear regression, if the design matrix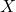 is not full rank, the covariance matrix 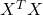can be singular, leading to numerical problems. L2 regularization addresses this by always adding a positive value, making the matrix invertible.

Best Practices:

• Parameter Tuning:
  The choice of (\lambda) is critical. Cross-validation techniques (e.g., k-fold cross-validation) can be used to find the optimal (\lambda) that minimizes overfitting while maintaining predictive performance.
• Normalization:
  Before applying L2 regularization, it’s often a good idea to normalize the features, especially since Ridge Regression assumes that all features contribute equally. StandardScaler or MinMaxScaler from Scikit-Learn can be used for this purpose.

By incorporating these strategies, L2 Regularization/Ridge Regression provides a robust and effective means of improving the robustness and accuracy of AI models. For more detailed information, refer to the Scikit-learn Implementation of Ridge Regression.

Dropout: Enhancing Neural Networks’ Generalization

Dropout is a simple yet powerful regularization technique aimed at improving the generalization of neural networks. It works by randomly “dropping out” (setting to zero) a subset of neurons within the network during the training process. This randomness forces the network to learn redundant representations of the data, thereby reducing its reliance on specific neurons and preventing overfitting.

How Dropout Works

During training, dropout temporarily removes selected neurons along with their connections. This process is probabilistic: each neuron is retained in the network with a given probability ( p ) (commonly 0.5 for hidden layers and 1.0 for the output layer). The mathematical representation of applying dropout to a neuron is as follows:

where represents the output after applying dropout, is the original output, and is a binary vector defined by the dropout probability.

For example, consider a simple neural network layer implementation in Python using TensorFlow:

import tensorflow as tf

# Defining a neural network layer with dropout
model = tf.keras.Sequential([
    tf.keras.layers.Dense(128, activation='relu', input_shape=(input_dim,)),
    tf.keras.layers.Dropout(0.5),  # Applying a 50% dropout
    tf.keras.layers.Dense(10, activation='softmax')
])

In the above example, a dropout layer with a 50% rate is added after the first dense layer. At each training step, this layer will randomly set 50% of its input units to zero.

Benefits of Dropout

1. Reduces Overfitting: Since dropout prevents any single neuron from becoming too important, the model is less likely to overfit. This leads to improved performance on unseen data.
2. Efficient Training: Dropout provides a form of model averaging where multiple models with different structures are trained simultaneously.
3. Minimal Computation Overhead: Implementing dropout requires minimal computational resources and adds only a little overhead to the training process.

Dropout Implementation in Different Frameworks

PyTorch Example:

import torch.nn as nn

# Define a neural network with dropout in PyTorch
class NeuralNet(nn.Module):
    def __init__(self):
        super(NeuralNet, self).__init__()
        self.fc1 = nn.Linear(input_dim, 128)
        self.dropout = nn.Dropout(p=0.5)
        self.fc2 = nn.Linear(128, 10)
    
    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.dropout(x)  # Applying dropout
        x = torch.softmax(self.fc2(x), dim=1)
        return x

Fine-Tuning Dropout Probability

Choosing the dropout probability ( p ) is crucial. Values typically range from 0.2 to 0.5, but the optimal choice depends on the specific dataset and model architecture. A too-high dropout rate may lead to underfitting, where the network fails to learn the data adequately. Cross-validation is often used to fine-tune the dropout rate.

For further reading, see the TensorFlow documentation on Dropout here and the PyTorch documentation on Dropout here.

By leveraging dropout, neural networks can achieve better generalization, ensuring they perform well not only on the training data but also on new, unseen datasets.

Role of Cross-Validation in Overfit Prevention

Cross-validation represents a critical tool in the arsenal for preventing overfitting in AI model training. By assessing the model’s performance across multiple folds or subsets of the dataset, cross-validation ensures that the model’s ability to generalize to unseen data is accurately evaluated.

At its core, cross-validation involves partitioning the dataset into complementary subsets and training the model multiple times, each time using a different subset for validation and the remaining subsets for training. The most commonly used form of cross-validation is k-fold cross-validation, where the dataset is divided into k equally sized folds. For instance, in a 5-fold cross-validation, the dataset is divided into five parts, and the model is trained and validated five times, each time using a different part for validation while the other four parts are used for training.

from sklearn.model_selection import KFold, cross_val_score
from sklearn.linear_model import Ridge  # Example model using L2 regularization
import numpy as np
from sklearn.datasets import make_regression

# Generate synthetic data for demonstration
X, y = make_regression(n_samples=100, n_features=20, noise=0.1)

# Define model
model = Ridge(alpha=1.0)

# Choose k for k-fold cross-validation
kf = KFold(n_splits=5, shuffle=True, random_state=42)

# Perform cross-validation
scores = cross_val_score(model, X, y, cv=kf, scoring='neg_mean_squared_error')
print("Cross-validation scores: ", scores)
print("Mean cross-validation score: ", np.mean(scores))

The results of the above script provide a measure of the model’s performance and its variability. The mean cross-validation score gives an overall sense of how well the model is likely to perform on new, unseen data.

Additionally, cross-validation can highlight issues such as high variance in the model, suggesting elements of overfitting. If the variance in scores across different folds is high, it indicates that the model might be highly sensitive to the specific data it was trained on, a classic overfitting symptom.

Variations of cross-validation, such as stratified k-fold cross-validation, cater to particular data characteristics. In cases where the data is imbalanced, stratified k-fold ensures that each fold maintains the proportionate distribution of the classes, providing a more reliable evaluation of the model’s performance.

from sklearn.model_selection import StratifiedKFold

# Example placeholder for classification data and labels
# Assuming `X` is feature data and `y` are the labels
# StratifiedKFold ensures the class distribution is maintained in each fold
stratified_kf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)

# Cross-validation using stratified k-fold
stratified_scores = cross_val_score(model, X, y, cv=stratified_kf, scoring='accuracy')
print("Stratified cross-validation scores: ", stratified_scores)
print("Mean stratified cross-validation score: ", np.mean(stratified_scores))

Cross-validation also facilitates the tuning of hyperparameters using techniques such as grid search cross-validation. This approach systematically evaluates a range of hyperparameters and selects the combination that yields the best cross-validated performance.

from sklearn.model_selection import GridSearchCV

# Define a parameter grid for the Ridge model
param_grid = {'alpha': [0.1, 1.0, 10.0, 100.0]}

# Grid search with k-fold cross-validation
grid_search = GridSearchCV(Ridge(), param_grid, cv=kf, scoring='neg_mean_squared_error')
grid_search.fit(X, y)

print("Best parameters: ", grid_search.best_params_)
print("Best cross-validated score: ", grid_search.best_score_)

By employing cross-validation as a standard practice, data scientists can obtain a robust estimate of their model’s performance and greatly mitigate the risk of overfitting, thereby enhancing the model’s ability to generalize to new, unseen data. This makes cross-validation an indispensable component in the toolkit for overfit prevention in AI models.

Combining Regularization Techniques for Optimal AI Performance

For AI models, combining regularization techniques can enhance performance by addressing overfitting through multiple avenues. Overfitting happens when a model performs exceptionally well on training data but poorly on unseen data, typically caused by learning noise and fluctuations in the training set. To mitigate this, using a multi-faceted approach is often the best strategy.

One common combination is integrating L2 regularization (Ridge regression) with dropout in neural networks. L2 regularization penalizes large weights by adding a term (\lambda \sum_i w_i^2) to the loss function, where (w_i) are the weights and (\lambda) is the regularization parameter. This helps in constraining the model complexity and prevents any single weight from exerting too much influence. On the other hand, dropout randomly sets a fraction of the neuron activations to zero during training, which forces the network to be more robust and prevents co-adaptation of neurons. Here is an example of how to implement these in a neural network using TensorFlow:

import tensorflow as tf

model = tf.keras.Sequential([
    tf.keras.layers.Dense(128, activation='relu', kernel_regularizer=tf.keras.regularizers.l2(0.01)),
    tf.keras.layers.Dropout(0.5),
    tf.keras.layers.Dense(64, activation='relu', kernel_regularizer=tf.keras.regularizers.l2(0.01)),
    tf.keras.layers.Dropout(0.5),
    tf.keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

In this setup, the Dense layers employ L2 regularization while the Dropout layers set 50% of the neurons to zero at each update during training time.

Another effective combination is L1 and L2 regularization together, often referred to as Elastic Net regularization. This approach leverages the strengths of both L1 and L2 regularization, where L1 regularization encourages sparsity (many weights becoming zero), and L2 regularization ensures that some weights are reduced but not entirely eliminated. The Elastic Net is beneficial for models dealing with highly correlated predictors. Here is an example of Elastic Net applied within a linear regression context using scikit-learn:

from sklearn.linear_model import ElasticNet

# Assuming X_train and y_train are your training data and labels
elastic_net = ElasticNet(alpha=1.0, l1_ratio=0.5)  # l1_ratio = 0.5 balances L1 and L2 regularization
elastic_net.fit(X_train, y_train)

In this instance, alpha is the combined regularization parameter, and l1_ratio determines the mix between L1 and L2 regularization.

When dealing with large and complex datasets, it’s essential to employ cross-validation alongside these regularization methods to ensure that your model generalizes well. By performing k-fold cross-validation, where the dataset is partitioned into k subsets and the model is trained k times, each time using a different subset as the test set and the remaining as the training set, you can systematically evaluate the efficacy of your regularization strategy. Combining regularization techniques addresses overfitting from multiple fronts, making your AI models more robust, generalizable, and performant across a range of tasks.