In the fast-evolving world of artificial intelligence and machine learning, efficient optimization techniques are crucial for developing robust and accurate models. Among these, gradient descent stands out as one of the most widely used and effective methods. This article delves into the core mechanics of gradient descent, exploring its various techniques and applications in AI optimization. Whether you’re optimizing neural networks in deep learning or fine-tuning algorithms for supervised or unsupervised learning, understanding gradient descent is fundamental to advancing your knowledge and improving your models’ performance. Let’s dive into the intricacies of this essential optimization algorithm and uncover how it powers much of modern artificial intelligence.
1. The Fundamentals of Gradient Descent
Gradient descent is one of the cornerstone optimization algorithms in machine learning and artificial intelligence. It is a first-order iterative optimization algorithm used to minimize a function by iteratively moving towards the minimum value of the function.
At its core, the primary goal of gradient descent is to find the local (or global) minimum of a function – typically the cost or loss function in a machine learning model. The cost function quantifies how well the model is performing in terms of error; therefore, minimizing this function enhances the model’s performance on given tasks.
Conceptual Breakdown:
- Initial Parameters:
The process begins with an initial set of parameters, often randomly generated. These parameters could be weights in a neural network, coefficients in a regression model, or any other variables used within the model. - Compute Gradient:
For a given set of parameters, calculate the gradient (also known as the derivative) of the cost function with respect to the parameters. The gradient points in the direction of the steepest ascent, so moving in the opposite direction should move us towards the minimum.Mathematically, for a parameter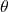 , the gradient is denoted as
, the gradient is denoted as 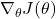 , where
, where 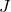 is the cost function.
is the cost function. - Update Parameters:
Adjust the parameters by moving them slightly in the direction opposite to the gradient. This is done by subtracting the product of the gradient and a predefined step size called the learning rate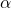 :
:![Rendered by QuickLaTeX.com \[ \theta := \theta - \alpha \nabla_\theta J(\theta) \]](https://codevibes.net/wp-content/ql-cache/quicklatex.com-e2d7c44debcfe139f13e6ee2c9fc8fa9_l3.png)
Here,
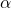 controls the size of the steps taken towards the minimum.
controls the size of the steps taken towards the minimum. - Iterate Until Convergence:
Repeat the process of computing gradients and updating parameters until the algorithm converges to a minimum. Convergence is typically defined by either a predetermined number of iterations or when changes to the cost function or parameters fall below a certain threshold.
Algorithm in Pseudocode:
Initialize parameters theta
Repeat until convergence:
Compute gradient: grad = gradient(J, theta)
Update parameters: theta = theta - alpha * grad
Detailed Example in Python using Numpy:
import numpy as np
# Hypothetical cost function J
def cost_function(theta, X, y):
return np.sum((X.dot(theta) - y) ** 2) / (2 * len(y))
# Gradient of the cost function
def compute_gradient(theta, X, y):
return X.T.dot(X.dot(theta) - y) / len(y)
# Gradient Descent Algorithm
def gradient_descent(X, y, theta, learning_rate, iterations):
history = []
for _ in range(iterations):
gradient = compute_gradient(theta, X, y)
theta = theta - learning_rate * gradient
cost = cost_function(theta, X, y)
history.append(cost)
return theta, history
# Sample data: X (features), y (target)
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3
# Initial Parameters
theta = np.random.randn(2)
learning_rate = 0.01
iterations = 1000
theta, history = gradient_descent(X, y, theta, learning_rate, iterations)
Mathematical Insight:
Consider a simple linear regression scenario where our cost function ( J ) is the Mean Squared Error (MSE):
![]()
where ![]() is the hypothesis (predicted value),
is the hypothesis (predicted value), ![]() is the input feature, and
is the input feature, and ![]() is the actual output.
is the actual output.
Gradient descent aims to find the ( \theta ) that minimizes this cost function. The gradient ( \nabla_\theta J(\theta) ) would be:
![]()
By iteratively updating ( \theta ) using the computed gradient and a learning rate, the algorithm converges towards the optimal solution ( \theta ).
References:
- Original paper by Cauchy (1847) on gradient descent[https://www.jstor.org/stable/2322795]
- Andrew Ng’s Cost Function and Gradient Descent Lecture Notes[https://see.stanford.edu/materials/aimlcs229/cs229-notes1.pdf]
This fundamental understanding of gradient descent is crucial for exploring its various techniques, optimization in neural networks, and other advanced AI algorithms.
2. How Gradient Descent Optimizes Neural Networks
When it comes to optimizing neural networks, gradient descent is one of the most effective and widely used optimization algorithms. Neural networks function as a series of interconnected nodes or neurons, organized into layers. Each of these layers has parameters—weights and biases—that need to be optimized to minimize the error in predictions. Gradient descent plays a crucial role in adjusting these parameters to improve the network’s overall accuracy.
Forward and Backward Pass
Optimizing neural networks using gradient descent involves two main steps: the forward pass and the backward pass. During the forward pass, the input data is passed through the network layer-by-layer to produce a prediction. Based on this prediction and the actual output, a cost function (or loss function) computes the error.
In the backward pass, gradient descent comes into play. This phase involves calculating the gradient of the cost function concerning each weight. By using these gradients, the algorithm updates the weights in the opposite direction of the gradient. This step lowers the cost function, effectively optimizing the network.
Backpropagation
Backpropagation is the algorithm used to compute these gradients efficiently. It uses the chain rule of calculus to propagate the gradient backwards through the network, from the output layer to the input. Each weight in the network is updated according to its partial derivative of the loss function, calculated by:
![]()
where ![]() is the weight,
is the weight, ![]() is the learning rate, and
is the learning rate, and ![]() is the loss function.
is the loss function.
Example: Optimizing a Simple Neural Network with Gradient Descent
Consider a simple neural network with one hidden layer used to classify data. Below is a Python code snippet illustrating gradient descent in a neural network using TensorFlow:
import tensorflow as tf
# Build the model
model = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu', input_shape=(784,)),
tf.keras.layers.Dense(10, activation='softmax')
])
# Compile the model
model.compile(optimizer='sgd', # stochastic gradient descent
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# Train the model
history = model.fit(train_images, train_labels, epochs=5)
In the example above, the model uses the Stochastic Gradient Descent (SGD) optimizer. During each epoch, the weights are updated in the direction that reduces the loss function, thanks to the gradient descent algorithm.
Computational Efficiency and Convergence
Efficiency and proper convergence are critical in the optimization process. If the gradient descent updates the weights too significantly (high learning rate), it can overshoot the optimal parameter values, causing the model to diverge. Conversely, if the learning rate is too small, convergence to the optimal values becomes sluggish.
Modern frameworks like TensorFlow and PyTorch offer various gradient descent optimizers that improve computational efficiency, such as Adam, RMSprop, and Momentum-based methods. These optimizers often provide better convergence properties and are more robust to different learning rates.
Regularization Techniques
To prevent overfitting and improve generalization, neural networks optimization often incorporates regularization techniques like L1, L2 regularization, or dropout. These techniques add additional terms to the loss function, penalizing large weights or randomly dropping units and their connections during training, respectively.
model = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu', kernel_regularizer=tf.keras.regularizers.l2(0.01)),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(10, activation='softmax')
])
By fine-tuning these attributes—using gradient descent, appropriate learning rates, advanced optimizers, and regularization—neural networks can achieve optimal performance on complex tasks. Detailed information about optimizers and their implementations can be found in the TensorFlow documentation.
3. Variants of Gradient Descent Techniques
Section 3: Variants of Gradient Descent Techniques
Gradient descent, a cornerstone of machine learning optimization, is not a one-size-fits-all technique. Depending on the scenario, various adaptations and improvements have been introduced to enhance performance and convergence. Below, we delve into some of the most prevalent variants of gradient descent techniques.
3.1. Batch Gradient Descent
Also known as Vanilla Gradient Descent, this variant involves computing the gradient of the cost function with respect to the complete dataset. While it guarantees convergence to the global minimum for convex functions (and to a local minimum for non-convex functions), its major downside is its inefficiency for large datasets due to the need to process all data points in each iteration.
# Example of Batch Gradient Descent in Python
def batch_gradient_descent(X, y, theta, learning_rate, iterations):
m = len(y)
for i in range(iterations):
gradient = X.T.dot(X.dot(theta) - y) / m
theta -= learning_rate * gradient
return theta
3.2. Stochastic Gradient Descent (SGD)
Stochastic Gradient Descent updates the parameters for each training example, thus it can be much faster than Batch Gradient Descent, especially on large datasets. However, the update directions can be noisy, leading to a more erratic (but often faster) convergence.
# Example of Stochastic Gradient Descent in Python
def stochastic_gradient_descent(X, y, theta, learning_rate, iterations):
m = len(y)
for i in range(iterations):
for j in range(m):
gradient = X[j, :].T * (X[j, :].dot(theta) - y[j])
theta -= learning_rate * gradient
return theta
3.3. Mini-Batch Gradient Descent
Mini-Batch Gradient Descent strikes a balance between Batch and Stochastic Gradient Descent by splitting the dataset into smaller batches. This allows for faster convergence compared to batch gradient descent and reduces the noisy gradient updates seen in SGD.
# Example of Mini-Batch Gradient Descent in Python
import numpy as np
def mini_batch_gradient_descent(X, y, theta, learning_rate, iterations, batch_size):
m = len(y)
for i in range(iterations):
indices = np.random.permutation(m)
X_shuffled = X[indices]
y_shuffled = y[indices]
for j in range(0, m, batch_size):
X_batch = X_shuffled[j:j+batch_size]
y_batch = y_shuffled[j:j+batch_size]
gradient = X_batch.T.dot(X_batch.dot(theta) - y_batch) / batch_size
theta -= learning_rate * gradient
return theta
3.4. Momentum
Momentum involves adding a fraction of the previous update vector to the current update. This helps accelerate SGD in the relevant direction and dampens oscillations.
# Example of Gradient Descent with Momentum in Python
def gradient_descent_momentum(X, y, theta, learning_rate, iterations, beta):
m = len(y)
velocity = np.zeros(theta.shape)
for i in range(iterations):
gradient = X.T.dot(X.dot(theta) - y) / m
velocity = beta * velocity + (1 - beta) * gradient
theta -= learning_rate * velocity
return theta
3.5. Adagrad
Adagrad adjusts the learning rate depending on the magnitude of the parameters’ previous gradients. The learning rate decreases for frequently occurring features, reducing the learning rate more drastically for infrequent updates.
# Example of Adagrad in Python
def adagrad(X, y, theta, learning_rate, iterations, epsilon=1e-8):
m = len(y)
gradient_squared_sum = np.zeros(theta.shape)
for i in range(iterations):
gradient = X.T.dot(X.dot(theta) - y) / m
gradient_squared_sum += gradient**2
theta -= (learning_rate / np.sqrt(gradient_squared_sum + epsilon)) * gradient
return theta
3.6. Adam (Adaptive Moment Estimation)
Adam combines the advantages of both RMSProp and Momentum. It computes adaptive learning rates for each parameter and maintains moving averages of the gradient and its square. Adam has been a game changer in neural network optimization due to its faster convergence.
# Example of Adam in Python
def adam(X, y, theta, learning_rate, iterations, beta1=0.9, beta2=0.999, epsilon=1e-8):
m = len(y)
m_t, v_t = np.zeros(theta.shape), np.zeros(theta.shape)
for i in range(1, iterations + 1):
gradient = X.T.dot(X.dot(theta) - y) / m
m_t = beta1 * m_t + (1 - beta1) * gradient
v_t = beta2 * v_t + (1 - beta2) * (gradient**2)
m_t_hat = m_t / (1 - beta1**i)
v_t_hat = v_t / (1 - beta2**i)
theta -= (learning_rate / (np.sqrt(v_t_hat) + epsilon)) * m_t_hat
return theta
These variants showcase the versatility and applicability of gradient descent across different problem domains, datasets, and computational constraints. For more details, visit the comprehensive documentation on gradient descent from TensorFlow and other reputable sources.
4. The Role of Learning Rate in Gradient Descent
The choice of learning rate is pivotal in controlling the optimization process in gradient descent techniques—a core component in training machine learning models. The learning rate, often denoted by η (eta), determines the size of the steps that the algorithm takes towards reaching the minimum of the loss function. Selecting an appropriate learning rate can significantly influence the performance and convergence speed of neural networks and other AI algorithms.
1. Importance of Learning Rate
A well-chosen learning rate allows the model to converge efficiently to the optimal solution. A too-high learning rate might cause the algorithm to overshoot the minimum, leading to divergence or oscillation around the minimum. Conversely, a too-low learning rate can result in an unnecessarily long training time, as the steps towards convergence become very small, causing the model to struggle with escaping local minima or saddle points.
2. Techniques for Selecting Learning Rate
- Grid Search and Random Search: Systematically or randomly selecting from a range of possible learning rates and comparing the performance of the model on a validation set.
- Learning Rate Schedules: Adjusting the learning rate during training according to a pre-defined scheme. Common schedules include:
- Step Decay: Reducing the learning rate by a factor at fixed intervals.
- Exponential Decay: Scaling the learning rate by an exponential function of the training epoch number.
- 1/t Annealing: Reducing the learning rate proportional to the inverse of the epoch number.
- Adaptive Learning Rates: Methods like Adam (Adaptive Moment Estimation) and RMSprop that adjust the learning rate for each parameter based on past gradients. These techniques often mitigate the need for extensive manual tuning.
import tensorflow as tf
# Example using Adam optimizer with an adaptive learning rate
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# Exponential decay of learning rate
initial_learning_rate = 0.1
lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay(
initial_learning_rate,
decay_steps=100000,
decay_rate=0.96,
staircase=True)
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=lr_schedule),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
3. Practical Considerations
- Warm-up Phases: Gradually increasing the learning rate from a lower value to the initially chosen learning rate over a few epochs to stabilize training in early stages.
- Cyclic Learning Rates: Oscillating the learning rate between two bounds instead of decaying it over time. This approach, suggested by Leslie N. Smith in 2017, can lead to faster convergence by allowing the model to escape potential saddle points.
Implementing these techniques can be instrumental for fine-tuning the gradient descent process, ensuring robust training of neural networks and improving overall model performance. For further details on implementing adaptive learning rates, refer to the TensorFlow documentation.
5. Challenges and Solutions in Gradient Descent Optimization
Gradient descent, while a powerful and widely-used optimization technique in AI, faces several challenges that can impact its effectiveness and efficiency. Addressing these challenges is crucial for achieving optimal performance in machine learning models.
5. Challenges and Solutions in Gradient Descent Optimization
1. Local Minima and Saddle Points
One significant challenge in gradient descent is navigating complex loss surfaces that contain multiple local minima and saddle points. Local minima are points where the gradient is zero, but they are not the global minimum. Saddle points, on the other hand, are points where the gradient is zero, but the point is not a minimum because it has regions of higher curvature in one direction and lower in another.
Solution:
- Random Restarts: Starting the gradient descent from multiple different initial points can help in avoiding poor local minima. The assumption is that at least one of these starting points will be closer to the global minimum.
- Advanced Techniques: Methods like simulated annealing or genetic algorithms can be used to escape local minima by exploring the parameter space more extensively.
2. Vanishing and Exploding Gradients
Gradients can sometimes become very small (vanishing gradients) or very large (exploding gradients) during training, especially in deep neural networks. This can lead to extremely slow convergence or divergence.
Solution:
- Gradient Clipping: This involves setting a threshold value, and components of the gradient that exceed this threshold are set to the threshold value. This helps in preventing exploding gradients. For more details, refer to the TensorFlow Gradient Clipping Documentation.
- Batch Normalization: This technique normalizes the inputs of each layer, which helps in maintaining consistent gradients. Refer to the Batch Normalization Paper for more information.
- Weight Initialization: Proper initialization strategies like Xavier or He initialization can also mitigate vanishing gradient problems.
3. Slow Convergence
Gradient descent can converge slowly if the path to the minimum is zigzagging or if the gradient takes very small steps.
Solution:
- Adaptive Learning Rates: Techniques such as AdaGrad, RMSprop, and Adam adjust the learning rate during training, speeding up convergence. You can read more about these techniques in the Adam Optimization Algorithm Paper.
- Momentum: This technique helps to accelerate gradients vectors in the right directions, leading to faster converging. You can add momentum to gradient descent as follows:
v = 0 beta = 0.9 for i in range(num_iterations): v = beta * v + (1 - beta) * gradient weights = weights - learning_rate * v
4. Choosing the Optimal Learning Rate
Selecting the right learning rate is crucial but challenging. A learning rate that is too high can cause the training process to overshoot the minimum, while a learning rate that is too low can make the training process very slow.
Solution:
- Learning Rate Scheduling: Techniques like exponential decay, step decay, or annealing can dynamically adjust the learning rate as the training progresses.
- Learning Rate Finder: An empirical approach involves trying different learning rates and observing which one performs best over a few epochs.
5. Computational Cost
Gradient descent, especially with large datasets, can be computationally expensive.
Solution:
- Stochastic Gradient Descent (SGD): Instead of computing the gradient over the entire dataset, SGD computes it over a small subset (mini-batch), drastically reducing computation time. Refer to Mini-Batch Gradient Descent for deeper insights.
- Parallel and Distributed Computing: Utilizing GPU, TPU, or distributed systems can also help in tackling the computational cost.
By understanding and addressing these challenges with appropriate solutions, gradient descent can remain an effective optimization tool in AI and machine learning applications.
6. Real-World Applications of Gradient Descent in AI
Gradient Descent is pivotal in a multitude of real-world AI applications, driving advancements and efficiency across various domains. One prominent application is in natural language processing (NLP), where models like BERT and GPT-3 use Gradient Descent to optimize language understanding and generation tasks. These models are trained on large corpora of text, and through Gradient Descent, they adjust millions of parameters to minimize errors in predicting the next word in a sequence or generate coherent text.
Another significant area where Gradient Descent is applied is computer vision, particularly in training convolutional neural networks (CNNs). Applications range from image classification, where the goal is to categorize images into predefined classes, to more complex tasks like object detection and segmentation. For example, models like ResNet and YOLO (You Only Look Once) use Gradient Descent to fine-tune weights so they can accurately identify objects within images. Training these deep learning models involves iterative optimization, where the loss function, often based on cross-entropy or mean squared error, is minimized to improve model accuracy.
In recommendation systems, such as those utilized by Netflix or Amazon, Gradient Descent is used to optimize collaborative filtering and matrix factorization techniques. These models predict user preferences by adjusting weights incrementally to minimize the difference between predicted and actual user ratings. By applying Gradient Descent, these recommendation systems become more accurate over time, thereby enhancing user experience and engagement.
Furthermore, Gradient Descent is integral to the field of autonomous driving. Neural networks trained for tasks like lane detection, pedestrian recognition, and path planning require optimization to ensure safety and efficiency. Autonomous vehicles leverage Gradient Descent algorithms to process real-time data from sensors and cameras, optimizing the decision-making process to navigate roads and avoid obstacles effectively.
In medical imaging, Gradient Descent helps in training models for disease diagnosis. Deep learning models, such as those used for detecting tumors in MRI scans or identifying diabetic retinopathy in retinal images, rely on Gradient Descent to adjust parameters and improve diagnostic accuracy. By minimizing loss functions related to diagnostic errors, these models provide more reliable outputs, aiding medical professionals in making informed decisions.
Moreover, Gradient Descent is crucial in financial market prediction, where neural networks analyze historical data to predict stock prices or market trends. Models trained using techniques like Long Short-Term Memory (LSTM) networks or Recurrent Neural Networks (RNNs) utilize Gradient Descent to optimize predictions by minimizing the discrepancy between predicted and actual market movements.
In summary, Gradient Descent’s applications span various fields, confirming its role as a cornerstone in the optimization of complex AI systems. Through continuous refinement of model parameters, Gradient Descent drives enhancements in performance, accuracy, and user experience across diverse AI-driven applications.
For more detailed information, you can refer to the documentation on optimizers in TensorFlow or the PyTorch official documentation which comprehensively cover the implementation and customization of Gradient Descent and its variants.