In the realm of data science and machine learning, linear regression stands as a foundational technique for analyzing and predicting relationships within datasets. Whether you are a novice looking for an introduction to linear regression or an experienced practitioner seeking advanced insights, understanding linear regression is crucial. This article dives deep into the core concepts and the practical implementation of linear regression, exploring its various forms from simple to multiple regression, and demonstrating its application using popular programming languages like Python and R. Join us as we unpack the intricacies of linear regression, shedding light on its utility and importance in the analytical toolkit.
Understanding Linear Regression: A Comprehensive Introduction
Linear regression is a cornerstone in the realms of statistics and machine learning, offering a straightforward yet powerful method for self-learning and predictions. At its core, linear regression is a technique used to model the relationship between a dependent (target) variable and one or more independent (predictive) variables. The objective is to find a linear equation that best fits the observed data, making it easier to predict the value of the target variable based on the known values of the predictors.
To develop a solid understanding of linear regression, it’s crucial to delve into both its theoretical foundations and practical applications. Grasping these concepts will enable you to effectively implement and interpret linear regression models, irrespective of the domain you work in.
Theoretical Foundation
The fundamental principle behind linear regression is the “least squares” method, which aims to minimize the sum of the squared differences between the observed and predicted values. Mathematically, the relationship can be represented as:
![]()
Where:
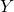 is the dependent variable.
is the dependent variable.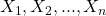 are the independent variables.
are the independent variables.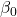 is the intercept.
is the intercept.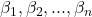 are the coefficients.
are the coefficients. is the error term.
is the error term.
Types of Linear Regression
There are two main types:
- Simple Linear Regression: Involves a single independent variable. The relationship is represented by a straight line.
![Rendered by QuickLaTeX.com \[ Y = \beta_0 + \beta_1X + \epsilon \]](https://codevibes.net/wp-content/ql-cache/quicklatex.com-d3fca7ed06b1e292066a41a68d7a3152_l3.png)
- Multiple Linear Regression: Involves two or more independent variables.
![Rendered by QuickLaTeX.com \[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n + \epsilon \]](https://codevibes.net/wp-content/ql-cache/quicklatex.com-2f5b1618a8dcdba7e519f94beab70a1d_l3.png)
Key Measures
Several statistical measures are essential for understanding the performance and validity of a linear regression model:
- Coefficient of Determination
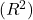 : Indicates the proportion of variance in the dependent variable that is predictable from the independent variables.
: Indicates the proportion of variance in the dependent variable that is predictable from the independent variables. - p-values: Assess the significance of each coefficient.
- F-Statistic: Tests the overall significance of the model.
Assumptions
Linear regression analysis is based on several assumptions:
- Linearity: The relationship between the dependent and independent variables should be linear.
- Independence: Observations should be independent.
- Homoscedasticity: The residuals (errors) should have a constant variance.
- Normality: The residuals should be normally distributed.
Violations of these assumptions can lead to unreliable estimates and misleading conclusions, hence the importance of diagnostics to check these assumptions.
Practical Implementation
While the theoretical backbone is essential, practical implementation cements understanding. For instance, in Python, libraries such as scikit-learn offer accessible tools for creating linear regression models. Here’s a succinct example:
from sklearn.linear_model import LinearRegression
import numpy as np
# Sample data
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3
# Create the model
model = LinearRegression().fit(X, y)
# Make predictions
predictions = model.predict(X)
# Outputs
print(f"Coefficients: {model.coef_}")
print(f"Intercept: {model.intercept_}")
print(f"Predictions: {predictions}")
For an in-depth comprehension, resources like the scikit-learn documentation provide further insights.
Common Pitfalls
Newcomers often face challenges such as overfitting, where the model captures noise instead of the signal. Regularization techniques like Ridge Regression and Lasso Regression help mitigate this by adding a penalty term to the loss function.
Understanding linear regression’s foundational principles sets the stage for more advanced topics such as Polynomial Regression, Logistic Regression, and other forms of statistical learning, forming a robust toolkit for data scientists and machine learning practitioners.
Key Concepts in Linear Regression: Variables, Assumptions, and Fitting
Linear regression is a fundamental algorithm in both statistics and machine learning that seeks to establish a linear relationship between dependent and independent variables. To get a deeper understanding of linear regression, it is essential to unpack its core concepts, such as types of variables, underlying assumptions, and methods of fitting a model.
Dependent and Independent Variables
In the context of linear regression, the dependent variable (often denoted as ![]() or the response variable) is the outcome that the model aims to predict. The independent variables (denoted as
or the response variable) is the outcome that the model aims to predict. The independent variables (denoted as ![]() or predictor variables) are the features used to make predictions. For example, in a simple linear regression model predicting house prices, the house price is the dependent variable, while predictors like square footage and number of bedrooms are the independent variables.
or predictor variables) are the features used to make predictions. For example, in a simple linear regression model predicting house prices, the house price is the dependent variable, while predictors like square footage and number of bedrooms are the independent variables.
Assumptions of Linear Regression
Linear regression models rest on several key assumptions that ensure the validity and reliability of the results. These are:
- Linearity: The relationship between the dependent and independent variables should be linear. This can be visually checked using scatter plots or residual plots.
- Independence: Observations should be independent of each other. Violation of this assumption often occurs in time series data, where past values can influence future values.
- Homoscedasticity: The variance of errors should be constant across all levels of the independent variables. Heteroscedasticity, when the spread of residuals is non-constant, can be detected using plots of residuals versus fitted values.
- Normality of Errors: The residuals (errors) of the model should be normally distributed. This assumption can be tested using statistical tests like the Shapiro-Wilk test or by visualizing the distribution of residuals with a Q-Q plot.
Fitting a Linear Regression Model
Fitting a linear regression model involves estimating the coefficients that minimize the difference between observed and predicted values. The most common method for this is Ordinary Least Squares (OLS), which minimizes the sum of the squared residuals (the differences between observed and predicted values).
Mathematical Formulation
The general linear regression model can be expressed as:
![]()
Here:
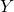 is the dependent variable.
is the dependent variable.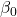 is the intercept.
is the intercept.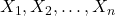 are the independent variables.
are the independent variables.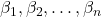 are the coefficients for the independent variables.
are the coefficients for the independent variables. is the error term.
is the error term.
Numerical Methods for Fit
While OLS is typically computed using closed-form solutions via matrix operations, numerical optimization methods like Gradient Descent can also be employed. Gradient Descent iteratively updates the coefficients to minimize the cost function, usually the Mean Squared Error (MSE).
Here’s a simplified example of how Gradient Descent might appear in Python:
import numpy as np
# Sample data
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
Y = np.dot(X, np.array([1, 2])) + 3
# Initialization
theta = np.random.randn(2, 1)
learning_rate = 0.01
iterations = 1000
for i in range(iterations):
gradients = 2 / len(X) * X.T.dot(X.dot(theta) - Y)
theta -= learning_rate * gradients
print("Fitted coefficients:", theta)
This code snippet shows a simple Gradient Descent loop to fit linear regression coefficients. For real-world datasets, packages like scikit-learn in Python or lm in R offer more efficient implementations.
Understanding these fundamental aspects of variables, assumptions, and fitting helps build a solid foundation for more complex topics in linear regression and ensures robust and reliable model building. For further details on assumptions and more advanced topics, the documentation for scikit-learn and statsmodels provides comprehensive resources.
Step-by-Step Linear Regression Tutorial: From Data Collection to Model Building
In this section, we’ll delve into a hands-on tutorial on linear regression, guiding you through each phase from data collection to model building. This will demonstrate how to implement linear regression using Python, allowing you to see each step in clear detail.
Step 1: Data Collection
Data collection is the foundational step of any data science project. For linear regression, you’ll need a dataset that contains both dependent and independent variables. Let’s suppose we are using a well-known dataset such as the California housing dataset available via scikit-learn.
from sklearn.datasets import fetch_california_housing
import pandas as pd
# Fetching the California housing dataset
data = fetch_california_housing()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['MedHouseVal'] = data.target # Adding target column
print(df.head())
Here, df is a DataFrame including multiple variables that could help predict the median house value (MedHouseVal).
Step 2: Data Preprocessing
After collecting the data, preprocessing is crucial to ensure the quality of your linear regression model. This involves handling missing values, encoding categorical variables, and normalizing the data.
For simplicity, we assume no missing values and no categorical variables in this dataset.
# Normalizing the data (an essential step for gradient-based methods)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
features = df.drop(columns='MedHouseVal')
scaled_features = scaler.fit_transform(features)
features = pd.DataFrame(scaled_features, columns=features.columns)
Step 3: Splitting Data into Training and Testing Sets
To evaluate the performance of our model, we need to split the data into training and test sets. This ensures we can validate the model on unseen data.
from sklearn.model_selection import train_test_split
X = features
y = df['MedHouseVal']
# Splitting the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
Step 4: Building the Linear Regression Model
Using scikit-learn, building a linear regression model is straightforward. The library’s LinearRegression class provides an easy-to-use implementation.
from sklearn.linear_model import LinearRegression
# Instantiate the model
model = LinearRegression()
# Fitting the model
model.fit(X_train, y_train)
Step 5: Making Predictions
With a trained model, we can now predict the target variable on the test dataset.
# Making predictions
y_pred = model.predict(X_test)
Step 6: Evaluating the Model
Model evaluation is crucial to understand how well your model performs. Common metrics include Mean Absolute Error (MAE), Mean Squared Error (MSE), and R-squared (R²).
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# Calculating evaluation metrics
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'MAE: {mae}')
print(f'MSE: {mse}')
print(f'R²: {r2}')
Step 7: Model Diagnostics
To ensure the reliability of your linear regression model, it’s essential to conduct diagnostic tests. Plotting residuals can help spotlight issues like non-linearity and heteroscedasticity.
import matplotlib.pyplot as plt
# Plotting residuals
residuals = y_test - y_pred
plt.scatter(y_pred, residuals)
plt.xlabel('Predicted Value')
plt.ylabel('Residuals')
plt.title('Residuals vs Fitted')
plt.axhline(y=0, color='r', linestyle='--')
plt.show()
References
This step-by-step linear regression tutorial gives you a practical guide from data collection to model building, including data preprocessing, model evaluation, and diagnostics in Python.
Simple vs. Multiple Linear Regression: Differences and Use Cases
Simple Linear Regression
Simple linear regression focuses on modeling the relationship between two variables: one independent (predictor) variable and one dependent (response) variable. The mathematical formula used is:
![]()
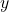 (Dependent Variable): The outcome or the variable we are trying to predict.
(Dependent Variable): The outcome or the variable we are trying to predict.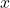 (Independent Variable): The predictor or the variable we use to predict
(Independent Variable): The predictor or the variable we use to predict 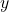 .
.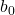 (Intercept): The value of
(Intercept): The value of 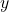 when
when 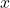 equals zero.
equals zero.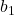 (Slope): The change in
(Slope): The change in 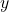 for a one-unit change in
for a one-unit change in 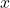 .
. (Error Term): The residual term capturing the deviations from the linear relationship.
(Error Term): The residual term capturing the deviations from the linear relationship.
Use Cases for Simple Linear Regression
- Predicting Trends: Estimating trends in stock prices based on time.
- Basic Economic Forecasting: Predicting consumer spending based on income level.
- Simple Sales Predictions: Predicting sales based on advertising spend.
- Medical Studies: Examining the effect of one medication dose on a particular health indicator.
Multiple Linear Regression
Multiple linear regression extends simple linear regression by incorporating multiple independent variables to predict the dependent variable. Its mathematical formula is:
![]()
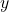 (Dependent Variable): The target variable we aim to predict.
(Dependent Variable): The target variable we aim to predict.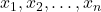 (Independent Variables): Multiple predictors used to estimate
(Independent Variables): Multiple predictors used to estimate 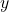 .
.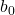 (Intercept): The expected value of
(Intercept): The expected value of 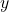 when all
when all 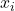 are zero.
are zero.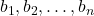 (Coefficients): The change in
(Coefficients): The change in 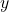 for a one-unit change in
for a one-unit change in 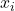 , holding other variables constant.
, holding other variables constant. (Error Term): The disturbance term capturing the unexplained variability.
(Error Term): The disturbance term capturing the unexplained variability.
Use Cases for Multiple Linear Regression
- Advanced Economic Forecasting: Predicting GDP growth based on multiple economic indicators.
- Real Estate Valuation: Estimating property prices using various features like location, size, and age.
- Marketing Analytics: Analyzing the effectiveness of different marketing channels (TV, online, print) on sales.
- Healthcare Predictions: Predicting patient outcomes based on multiple health metrics such as age, weight, and pre-existing conditions.
Practical Example in Python
Simple Linear Regression in Python
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# Generating sample data
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([1, 2, 3, 4, 5])
# Model instantiation and fitting
model = LinearRegression().fit(X, y)
# Making predictions
y_pred = model.predict(X)
# Plotting results
plt.scatter(X, y, color='blue')
plt.plot(X, y_pred, color='red')
plt.xlabel('Independent Variable')
plt.ylabel('Dependent Variable')
plt.title('Simple Linear Regression')
plt.show()
Multiple Linear Regression in Python
# Import necessary libraries
from sklearn.model_selection import train_test_split
# Generating sample data
data = {
'x1': [1, 2, 3, 4, 5],
'x2': [2, 4, 5, 6, 7],
'y': [1, 2, 3, 4, 5]
}
df = pd.DataFrame(data)
# Preparing data for model
X = df[['x1', 'x2']]
y = df['y']
# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# Model instantiation and fitting
model = LinearRegression().fit(X_train, y_train)
# Making predictions
y_pred = model.predict(X_test)
# Results
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)
By understanding the unique strengths of simple and multiple linear regression models, data scientists can better tailor their approach to specific problem domains.
Implementing Linear Regression in Python: A Practical Guide
To get hands-on experience with linear regression, let’s delve into its implementation in Python. Python offers several libraries that simplify this process, such as scikit-learn, statsmodels, and even numpy and scipy. For this guide, we’ll primarily use scikit-learn due to its simplicity and efficiency.
Setting Up Your Environment
Before we start coding, ensure you have Python and scikit-learn installed. You can achieve this via pip:
pip install numpy pandas scikit-learn matplotlib
We’ll also use numpy for handling arrays and pandas for data manipulation. matplotlib will be useful for visualizing the results.
Loading and Preparing Your Data
Let’s consider a dataset representing a linear relationship between the number of hours studied (feature) and the scores obtained (target). We’ll use pandas to load a sample dataset.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Generate simple linear data
np.random.seed(0)
X = 2.5 * np.random.randn(100) + 1.5
y = 2 * X + np.random.randn(100) * 0.5 + 1.5
data = pd.DataFrame({'Hours': X, 'Scores': y})
# Visualize the data
plt.scatter(data['Hours'], data['Scores'])
plt.xlabel('Hours Studied')
plt.ylabel('Scores')
plt.title('Hours Studied vs Scores')
plt.show()
Splitting the Data
It’s crucial to split your data into training and test sets to evaluate the model’s performance on unseen data.
from sklearn.model_selection import train_test_split
# Reshape data for scikit-learn
X = data['Hours'].values.reshape(-1, 1)
y = data['Scores'].values.reshape(-1, 1)
# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
Building the Linear Regression Model
Using scikit-learn, we can instantiate and fit our linear regression model:
from sklearn.linear_model import LinearRegression
# Create the model
model = LinearRegression()
# Train the model
model.fit(X_train, y_train)
# Output model parameters
print("Intercept:", model.intercept_)
print("Coefficient:", model.coef_)
Making Predictions
With the model trained, you can make predictions on the test set:
# Predicting using the model
y_pred = model.predict(X_test)
# Compare actual output values with predicted values
compare_df = pd.DataFrame({'Actual': y_test.flatten(), 'Predicted': y_pred.flatten()})
print(compare_df)
Evaluating the Model
To evaluate our linear regression model, we’ll measure metrics such as Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE):
from sklearn.metrics import mean_absolute_error, mean_squared_error
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
print("Root Mean Squared Error:", rmse)
Visualizing the Regression Line
Finally, visualize the best-fit regression line on your data:
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=2)
plt.xlabel('Hours Studied')
plt.ylabel('Scores')
plt.title('Regression Line: Hours Studied vs Scores')
plt.show()
By following these steps, you will have implemented a linear regression model in Python, understood how to split data, fit the model, and evaluate its performance. For more details on scikit-learn and linear regression, check the official documentation.
Analyzing Results: Interpreting Linear Regression Outputs
Once the linear regression model has been fit to your data, the next crucial step is to analyze and interpret the results. Understanding the outputs is vital to making meaningful inferences and decisions based on the model. Here, we delve into the most critical components you will encounter when analyzing linear regression outputs, with a focus on outputs from Python’s statsmodels and scikit-learn libraries.
Coefficients Interpretation
The coefficients (also known as weights) are fundamental to understanding the linear relationship between each independent variable and the dependent variable. For example, consider this output from the statsmodels library:
import statsmodels.api as sm
# Assuming X and y are already defined
model = sm.OLS(y, sm.add_constant(X)).fit()
print(model.summary())
You’ll see something like this in the summary:
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------
const 2.9382 0.311 9.445 0.000 2.320 3.556
X1 0.0017 0.000 4.121 0.000 0.001 0.003
X2 0.2000 0.052 3.865 0.000 0.098 0.302
- Coefficients (
coef): The coefficient value indicates how much the dependent variable is expected to increase when that independent variable increases by one, holding all other variables constant. - Standard Error (
std err): This measures the accuracy of the coefficient by indicating the extent of variability in the coefficient estimate. - t-Statistic (
t): Used to determine whether the coefficient is significantly different from zero. - p-Value (
P>|t|): This helps you understand the significance of each coefficient. A common threshold for significance is 0.05. - Confidence Intervals (
[0.025 0.975]): These provide a range within which we can be certain that the true coefficient value lies, with 95% confidence.
R-squared and Adjusted R-squared
Both scikit-learn and statsmodels compute R-squared values that we use to evaluate model performance:
from sklearn.metrics import r2_score
# Assuming y_test and y_pred are defined
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2}")
- R-squared: Indicates the proportion of the variance in the dependent variable that is predictable from the independent variables. However, it has limitations, such as increasing with more variables, irrespective of their relevance.
- Adjusted R-squared: Adjusts R-squared based on the number of predictors, providing a more accurate measure when dealing with multiple predictors.
Residuals Analysis
Evaluating the residuals—the differences between the observed and predicted values—is crucial for diagnosing model fit.
import matplotlib.pyplot as plt
# Assuming y and y_pred are defined
residuals = y - y_pred
plt.scatter(y_pred, residuals)
plt.xlabel('Predicted')
plt.ylabel('Residuals')
plt.title('Residuals vs Fitted')
plt.show()
- Homogeneity of variance: The residuals should display no clear pattern.
- Independence: Residuals should be randomly distributed.
- Normality: Residuals should follow a normal distribution, especially for small sample sizes.
Model Evaluation Metrics
For more comprehensive evaluation, especially when using scikit-learn, leverage different metrics available in sklearn.metrics:
from sklearn.metrics import mean_squared_error, mean_absolute_error
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")
print(f"Mean Absolute Error: {mae}")
- Mean Squared Error (MSE): Measures the average of the squares of the errors. It’s more sensitive to outliers.
- Mean Absolute Error (MAE): Measures the average magnitude of the errors in a set of predictions, without considering their direction. It provides a more balanced view.
Understanding Collinearity
High collinearity among variables can inflate standard errors and make coefficient estimates unstable. Variance Inflation Factor (VIF) can be a useful diagnostic tool here:
from statsmodels.stats.outliers_influence import variance_inflation_factor
# Assuming X is the design matrix
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)
- VIF Values: A VIF value exceeding 5-10 indicates high collinearity that may need addressing.
By understanding and correctly interpreting these outputs, you can effectively gauge how your model fits the data and make necessary adjustments. Accurate interpretation enables you to provide more reliable predictions and insights.
Real-World Applications of Linear Regression in Data Science and Machine Learning
Linear regression is a cornerstone statistical technique with a multitude of real-world applications in data science and machine learning. Here, we explore several practical applications where linear regression has made significant impact.
Predictive Analytics
Predictive analytics is one of the most common uses of linear regression. For example, in finance, linear regression models are employed to predict stock prices or economic indicators. By analyzing historical data, the model can forecast future values, guiding investment decisions and risk management.
Example:
A financial analyst might use multiple linear regression to predict stock prices based on variables such as trading volume, interest rates, and previous stock prices.
import pandas as pd
from sklearn.linear_model import LinearRegression
# Loading dataset
data = pd.read_csv('stock_prices.csv')
# Independent variables: Volume, Interest Rates, Previous Day’s Closing Price
X = data[['Volume', 'Interest_Rate', 'Previous_Close']]
# Dependent variable: Today's Closing Price
y = data['Today_Close']
# Building the model
model = LinearRegression()
model.fit(X, y)
# Predicting stock prices
predictions = model.predict(X)
Healthcare and Medical Research
Linear regression is particularly useful in the healthcare industry for medical research and patient care. For instance, it can model the relationship between patient health metrics and treatment outcomes.
Example:
Researchers might use linear regression to investigate how lifestyle factors (like exercise frequency, diet, and sleep) affect blood pressure levels.
# Assuming we have a dataset healthcare_data with columns Exercise, Diet, Sleep, and Blood_Pressure
model <- lm(Blood_Pressure ~ Exercise + Diet + Sleep, data = healthcare_data)
summary(model)
Marketing and Sales
In marketing, businesses use linear regression to understand and predict customer behavior. For example, it can model how advertising spend across different channels impacts sales.
Example:
A marketing analyst might employ multiple linear regression to gauge the effect of TV, radio, and online advertising on sales.
import numpy as np
import statsmodels.api as sm
# Loading dataset
marketing_data = pd.read_csv('marketing_sales.csv')
# Independent variables: TV, Radio, Online Advertising Spend
X = marketing_data[['TV', 'Radio', 'Online']]
# Dependent variable: Sales
y = marketing_data['Sales']
# Adding a constant for the intercept
X = sm.add_constant(X)
# Building the model
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
print(model.summary())
Environmental Studies
In environmental science, linear regression helps in understanding and predicting ecological patterns and climate change. It’s especially useful for modeling the relationship between atmospheric CO2 levels and global temperature change.
Example:
Environmental scientists might use simple linear regression to explore the correlation between CO2 levels and global average temperatures.
# Loading dataset
climate_data <- read.csv('climate_change.csv')
# Simple Linear Regression: CO2 Levels vs. Global Temperature Anomaly
model <- lm(Temperature_Anomaly ~ CO2_Levels, data = climate_data)
summary(model)
Sports Analytics
Linear regression has found a niche in sports analytics, where it’s employed to enhance team performance through data-driven decisions. Analysts use it to predict player performance based on metrics like training data, past performance, and physical health.
Example:
A sports analyst might use linear regression to predict the number of goals a soccer player will score in a season based on training hours, previous goals, and physical fitness level.
# Loading dataset
sports_data = pd.read_csv('soccer_player_stats.csv')
# Independent variables: Training Hours, Previous Goals, Fitness Level
X = sports_data[['Training_Hours', 'Previous_Goals', 'Fitness_Level']]
# Dependent variable: Goals this season
y = sports_data['Goals_Season']
# Building the model
model = LinearRegression()
model.fit(X, y)
# Predicting goals
predictions = model.predict(X)
These applications illustrate the versatility and power of linear regression in diverse fields, making it an indispensable tool in the arsenal of data scientists and machine learning practitioners.